Coherence in Large-Scale Networks:
Dimension Dependent Limitations of Local Feedback


Imagine large vehicular formations that need to travel in unison, something that resembles a rigid lattice or grid of objects. In nature, such formations are found in e.g. birds flying in formation or fish schooling together. One can also think of swarms of autonomous artificial vehicles attempting to form a rigid grid-like formation.
The Geese shown above in effect form a 1-dimensional "string formation". The picture in the middle is a caricature of a 2-dimensional artificial vehicle formation. Schools of fish appear to be 3-dimensional formations. If you've seen videos of such formations on something like the Discovery Channel, you probably have observed that fish schools appear to swim in much tighter formations than the somewhat meandering string formations of Geese. In other words, fish schools are more "coherent" than Geese formations, and it turns out that this is a fundamental pattern. 3-dimensional formations are more coherent than 1-dimensional ones when agents can only use local feedback to control their relative motion. It is also intuitively clear that the larger the formation is, the less likely it is to be coherent. These observations raise several questions:
  • How does one quantify "coherence", i.e. how closely does a formation resemble a rigid lattice? We refer to these as macroscopic performance measures.
  • How does one capture the local behavior of vehicles, such as the tendency to run into each other? We refer to these as microscopic performance measures.
  • How do these measures scale with formation size, and how do they depend on the network topology and underlying spatial dimension?
  • How does all this depend on whether vehicles have local feedback versus global feedback of things like position errors and velocity errors?

The answers to these questions are provided in the paper below. It turns out that a common phenomenon appears where a higher spatial dimension implies a more favorable scaling of coherence measures, with a dimensions of 3 being necessary to achieve coherence in consensus and vehicular formations under certain conditions.

The situation is worst in one dimension, e.g. in the so-called Vehicular Platoons problem. It turns out that it is impossible to have large coherent 1-dimensional vehicular platoons with only local feedback. Consider a simple control scheme for a toy platooning problem as shown here


The red arrows indicated stochastic forcing disturbances buffeting each vehicle. A simple control scheme based on look-ahead and look-behind policies can be easily designed to stabilize the entire formation (and avoid the so-called string instability problem, which incidentially is unrelated to the phenomenon we discuss here).
However, if you simulate the system, here's what you observe. The graph on the right shows the position trajectories of a 100 vehicle formation (relative to leader). It exhibits what can be described as an accordion-like motion in which large shape features in the formation fluctuate. We call this phenomenon a lack of formation coherence. It is only discernible when one "zooms out" to view the entire formation. The length of the formation fluctuates stochastically, but with a distinct slow temporal and long spatial wavelength signature.
In contrast, the zoomed-in view here shows a relatively well regulated vehicle-to-vehicle spacing. In general, it appears that small scale (both temporally and spatially) disturbances are well regulated, while large scale disturbances are not. An intuitive interpretation of this phenomenon is that local feedback strategies are unable to regulate against large scale disturbances in this one dimensional formation. This is an example of the lack of coherence in this formation.
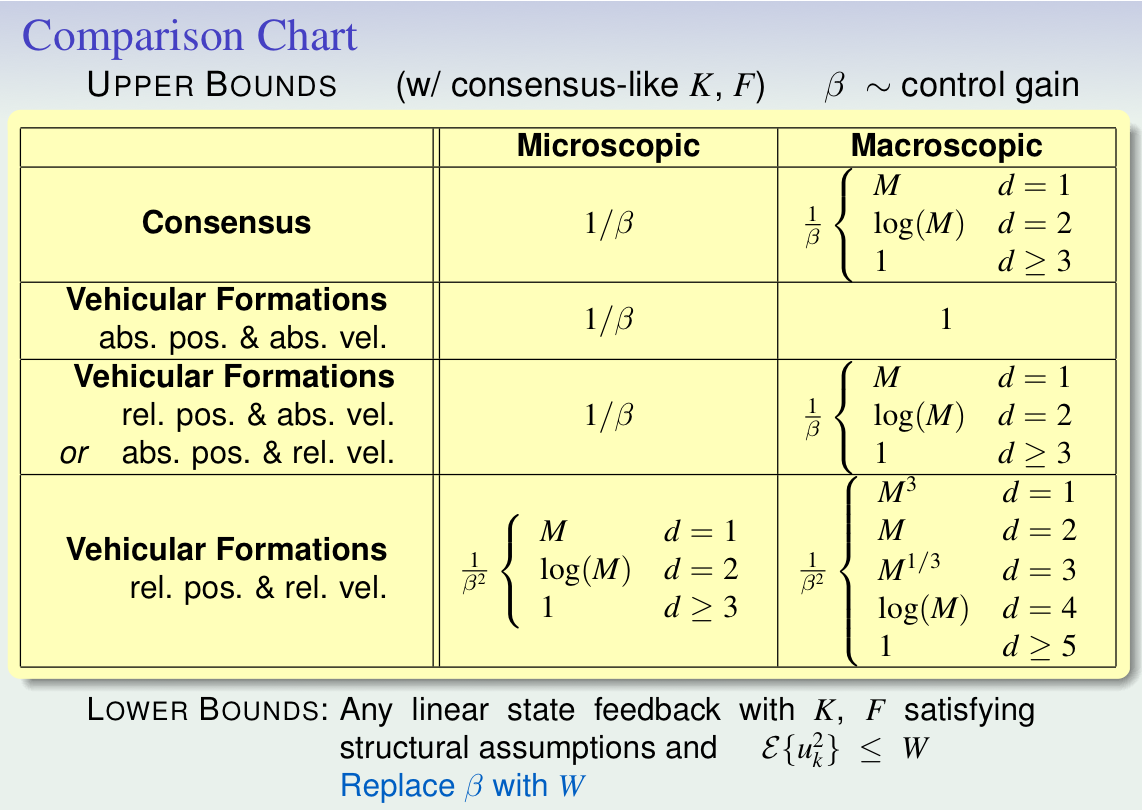
What is perhaps surprising is that in higher spatial dimensions, it is indeed possible to have coherent formations with only local feedback. The table below summarizes the asymptotic scalings of microscopic error measures and macroscopic measures of formation cohesion under various types of feedback controls.



The parameter beta in these tables can be understood as a measure of the control effort at each site.
For all the details, see the preprint:
  1. B. Bamieh, M. Jovanovic, P. Mitra, and S. Patterson. Coherence in Large-Scale Networks: Dimension Dependent Limitations of Local Feedback. Submitted to IEEE Trans. Aut. Cont., 2009. [bibtex-entry]



[BACK TO Pictures PAGE]