Control of Quantum Systems
There's much interest among certain control engineers, physicists and physical chemists in trying to integrate ideas from control design with those of quantum dynamics. The applications range from laser chemistry (molecular vibrations control with femtosecond laser pulses) and NMR (nuclear spin control) to quantum computing.
As a control problem, the dynamics are governed by the Schroedinger equation
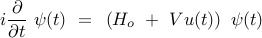
where u(t) is an external (control) signal (e.g. an electromagnetic field strength in the laser
chemistry case, or a magnetic field in the NMR case), 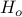 is the nominal (internal) Hamiltonian,
and
is the nominal (internal) Hamiltonian,
and 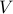 is the “control” Hamiltonian representing the coupling of the external control to the
internal dynamics (e.g. dipole moment coupling). Notice that this is a so-called “bilinear system”.
These equations look deceptively simple. However, this hides the fact that infinite-dimensional
bilinear systems are a universal class representing effectively all dynamical systems with an
input (see “Myths, ….” in the talks page).
is the “control” Hamiltonian representing the coupling of the external control to the
internal dynamics (e.g. dipole moment coupling). Notice that this is a so-called “bilinear system”.
These equations look deceptively simple. However, this hides the fact that infinite-dimensional
bilinear systems are a universal class representing effectively all dynamical systems with an
input (see “Myths, ….” in the talks page).
Optimal State Transfer
 |
One of the simplest problems to pose is that of optimal population transfer: find the optimal
control |
Time-scale Separation in Optimal Control
In fact one can be much more precise. We can show that in the limit of large transfer times 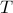 ,
the optimal control has the following form
,
the optimal control has the following form
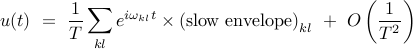
where the exponential term represents the Bohr frequency between the 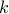 and
and 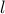 states of the system.
Thus, up to first order in
states of the system.
Thus, up to first order in 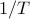 , the optimal control is of the form of Bohr frequencies modulated
by slowly varying (realtive to the time scale
, the optimal control is of the form of Bohr frequencies modulated
by slowly varying (realtive to the time scale 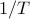 ) envelopes.
This makes precise the notion of time scale separation for such problems, and
reduces the optimal control problem (for
) envelopes.
This makes precise the notion of time scale separation for such problems, and
reduces the optimal control problem (for 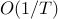 terms) to that of designing the envelopes.
The slow envelopes obey
optimal-control-type differential equations (which are derived via an averaging procedure)
that are orders of magnitude less stiff than the original ones, and thus much easier to obtain numerically.
terms) to that of designing the envelopes.
The slow envelopes obey
optimal-control-type differential equations (which are derived via an averaging procedure)
that are orders of magnitude less stiff than the original ones, and thus much easier to obtain numerically.
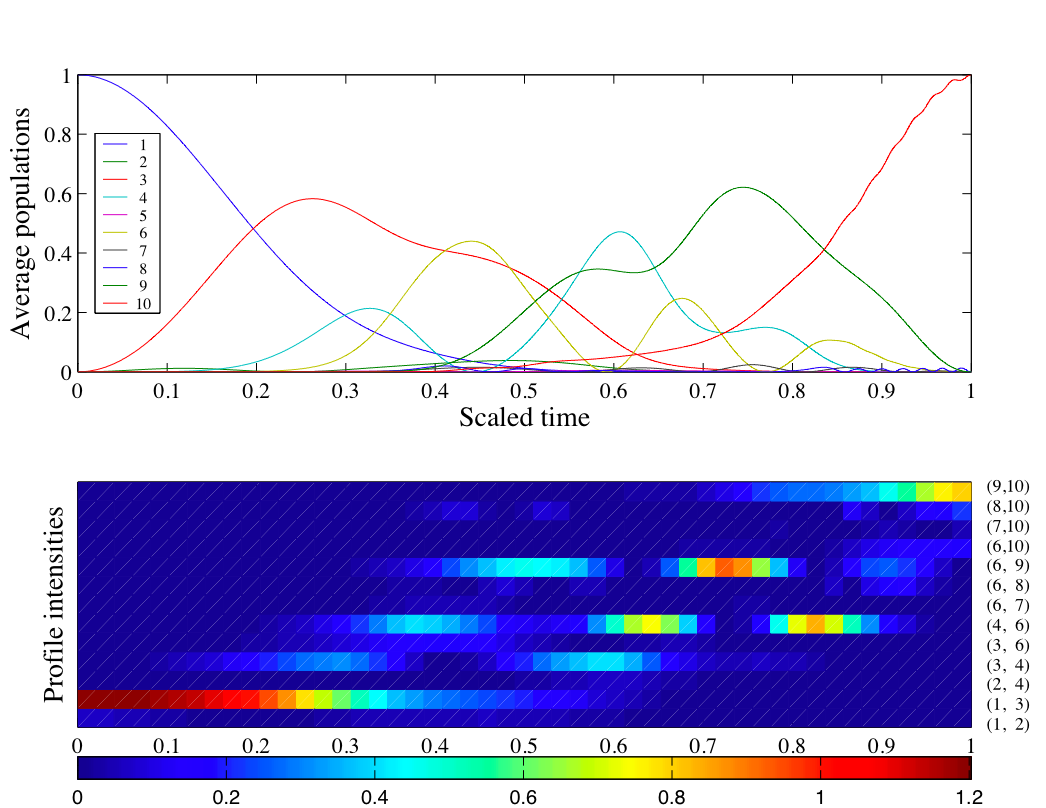 |
The picture shows a cartoon spectrogram of the control signal and the respective state populations for a 10 state representation of the quantum Morse oscillator. This particular control transitions from the ground state (1st state) to the 10th state. The spectrogram (bottom) is labeled by the Bohr frequencies (labeled by the corresponding transitions rather than the actual frequency). Notice that there's no component for the (1,10) transition Bohr frequency, but a collection of intermediate transitions. One can intuitively think of the optimal control algorithm as providing an optimally timed schedule of intermediate transitions. |
Related Papers
Optimal Population Transfers in Quantum Systems for Large Transfer Time, S. Grivopoulos and B. Bamieh, IEEE Trans. on Automatic Control, 53(4):980-992, May 2008.
Lyapunov Based Control of Quantum Systems, S. Grivopoulos and B. Bamieh, Proceedings. 42nd IEEE Conference on Decision and Control (CDC), 2003.
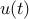 to transfer the system from one given state to another while minimizing
control energy.
Actually, this problem
turns out to be very hard to solve for large quantum systems (read: molecules
with two or more bonds). Except for very simple cases, it can only be solved
numerically, and even then, one is only guaranteed to converge to local minima. None the less, numerical
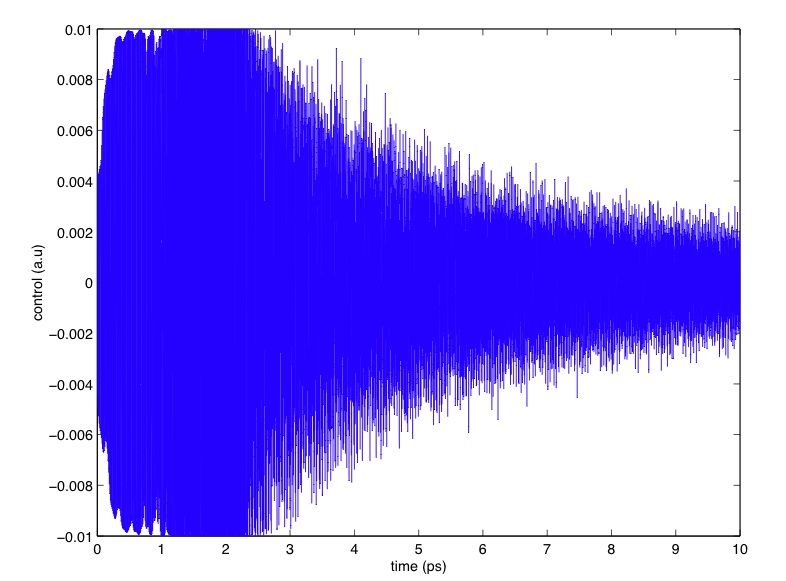
algorithms provide some insight. The picture to the left is that of a candidate control signal for a
quantum Morse oscillator system with dipole moment coupling.
Such signals look very complex, but if one looks at its spectrogram (i.e.
a time-frequency decomposition), one sees that it is composed of weighted combinations of
Bohr frequencies with time varying weights.
to transfer the system from one given state to another while minimizing
control energy.
Actually, this problem
turns out to be very hard to solve for large quantum systems (read: molecules
with two or more bonds). Except for very simple cases, it can only be solved
numerically, and even then, one is only guaranteed to converge to local minima. None the less, numerical
algorithms provide some insight. The picture to the left is that of a candidate control signal for a
quantum Morse oscillator system with dipole moment coupling.
Such signals look very complex, but if one looks at its spectrogram (i.e.
a time-frequency decomposition), one sees that it is composed of weighted combinations of
Bohr frequencies with time varying weights.