View Factor Calculation

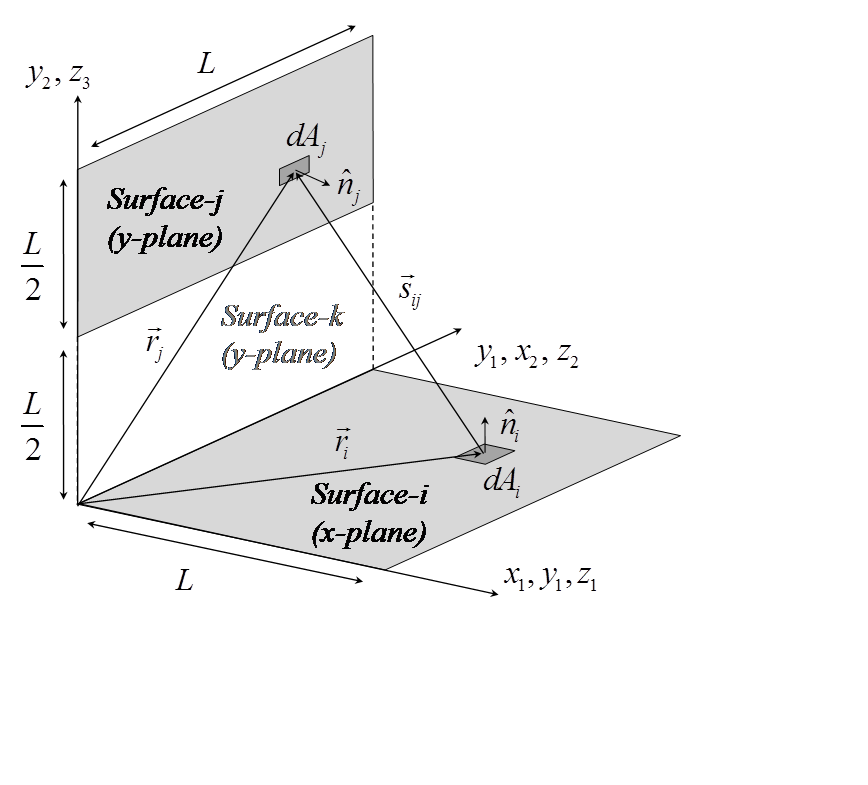To demonstrate the use of FijCalcView( ), consider the task of numerically integrating for the view factor between the two surfaces labeled surface-i and surface-j in the illustration

 

The vector r_i sweeping out the area A_i (in the x-plane) is given by:

                                                             ,

where                                           .

The unit normal and area of dA_i are given by:

                                                             

and                                                       .

 

Similarly, the vector r_j sweeping out the area A_j (in the y-plane), is given by:

                                                            ,

where                                         .

The unit normal and area of dA_j are given by:

                                                               

and                                                       .

 

The information about the integration task is provided with the definitions:

L=1;

ri=@(x)[x(1), x(2), 0];

spani=[0, L; 0, L];

ni=@(x)[0, 0, 1];

dAi=@(x,dx)dx(1)*dx(2);

 

rj=@(y)[0, y(1), y(2)];

spanj=[0, L; L/2, L];

nj=@(y)[1, 0, 0];

dAj=@(y,dy)dy(1)*dy(2);  

 

The view factor is calculated with the integration task subdivided into 15 numerical steps for each spatial direction on each surface:

[Fij Ai]=FijCalcView(spani,ri,ni,dAi,spanj,rj,nj,dAj,15)

Fij =  0.053958

Ai =  1.000

 

This result can be confirmed with the analytic function CornerView( ):

L=1;

Fi_jk=CornerView(L,L,L);

Fik=  CornerView(L,L,L/2);

Fij=Fi_jk-Fik

Fij =  0.053857