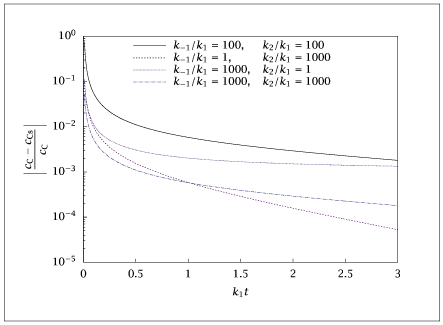
Figure 5.12:

Fractional error in the QSSA concentration of C versus dimensionless time for the series-parallel reaction, A<-> B-> C.

Code for Figure 5.12

Text of the GNU GPL.

main.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
% Copyright (C) 2001, James B. Rawlings and John G. Ekerdt
%
% This program is free software; you can redistribute it and/or
% modify it under the terms of the GNU General Public License as
% published by the Free Software Foundation; either version 2, or (at
% your option) any later version.
%
% This program is distributed in the hope that it will be useful, but
% WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
% General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program; see the file COPYING.  If not, write to
% the Free Software Foundation, 59 Temple Place - Suite 330, Boston,
% MA 02111-1307, USA.

% This program "schm2_error.m" generates error curves for the
% reversible series problems as the reverse rate consant and
% the second rate constant are varied.  First-order reactions

% Last edited 1/30/97.

% Revised 7/24/2018

p = struct(); % Create structure to pass parameters to ode15s function
p.k1 = 1.0;


Initial = [1,0,0]';
t = [0:.01:3]';
t_tmp = t(2:length(t));

%
p.k_1 = 100;
p.k2 = 100;
opts = odeset ('AbsTol', sqrt (eps), 'RelTol', sqrt (eps));

[tsolver, solution] = ode15s(@(t,x) rxrate(t,x,p),t,Initial,opts);
alpha = (p.k1*p.k2)/(p.k_1 + p.k2);
c_Css = 1-exp(-alpha*t_tmp);
c_Cexact = solution(2:end,3);
E = (c_Cexact - c_Css)./c_Cexact;
EE = abs(E);
error = log10(EE);
%answer3 = [t_tmp error];
% JBR, 2/22/98
answer3 = [t_tmp EE];

%
p.k_1 = 1;
p.k2 = 1000;

[tsolver, solution] = ode15s(@(t,x) rxrate(t,x,p),t,Initial,opts);
alpha = (p.k1*p.k2)/(p.k_1 + p.k2);
c_Css = 1-exp(-alpha*t_tmp);
c_Cexact = solution(2:end,3);
E = (c_Cexact - c_Css)./c_Cexact;
EE = abs(E);
error = log10(EE);
%answer3 = [answer3 error];
% JBR, 2/22/98
answer3 = [answer3 EE];

%
p.k_1 = 1000;
p.k2 = 1;

[tsolver, solution] = ode15s(@(t,x) rxrate(t,x,p),t,Initial,opts);
alpha = (p.k1*p.k2)/(p.k_1 + p.k2);
c_Css = 1-exp(-alpha*t_tmp);
c_Cexact = solution(2:end,3);
E = (c_Cexact - c_Css)./c_Cexact;
EE = abs(E);
error = log10(EE);
%answer3 = [answer3 error];
% JBR, 2/22/98
answer3 = [answer3 EE];

%
p.k_1 = 1000;
p.k2 = 1000;

[tsolver, solution] = ode15s(@(t,x) rxrate(t,x,p),t,Initial,opts);
alpha = (p.k1*p.k2)/(p.k_1 + p.k2);
c_Css = 1-exp(-alpha*t_tmp);
c_Cexact = solution(2:end,3);
E = (c_Cexact - c_Css)./c_Cexact;
EE = abs(E);
error = log10(EE);
%answer3 = [answer3 error];
% JBR, 2/22/98
answer3 = [answer3 EE];

save -ascii schm2_error.dat answer3;

if (~ strcmp (getenv ('OMIT_PLOTS'), 'true')) % PLOTTING
    semilogy (answer3(:,1),answer3(:,2:5));
    % TITLE
end % PLOTTING

rxrate.m

1
2
3
4
5
6
7
8
9
function dcdt = rxrate(t,x,p)
   c1 = x(1);
   c2 = x(2);
   c3 = x(3);

   r1 = p.k1*c1 - p.k_1*c2;
   r2 = p.k2*c2;

   dcdt = [-r1; r1-r2; r2];