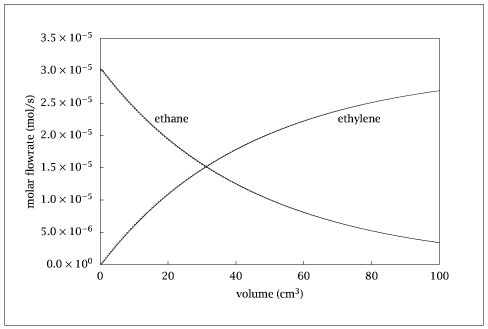
Figure 5.15:

Comparison of the molar flowrates of C_2H_6 and C_2H_4 for the exact solution (solid lines) and the simplified kinetic scheme (dashed lines).

Code for Figure 5.15

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
% Copyright (C) 2001, James B. Rawlings and John G. Ekerdt
%
% This program is free software; you can redistribute it and/or
% modify it under the terms of the GNU General Public License as
% published by the Free Software Foundation; either version 2, or (at
% your option) any later version.
%
% This program is distributed in the hope that it will be useful, but
% WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
% General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program; see the file COPYING.  If not, write to
% the Free Software Foundation, 59 Temple Place - Suite 330, Boston,
% MA 02111-1307, USA.

% This program solves part of ethane pyrolysis example that is in the
% text.  It plots the exact and the simple solutions
% It is titled ethane_comparison.m
%
% It was last edited 2/5/97
%
% Revised 7/24/2018

%E in Joules, mass in grams, T in Kelvin, time in sec, volume in cm3


Components_1 = [' C2H6 = 1,',' CH3 = 2,',' CH4 = 3,',' C2H5 = 4'];
Components_2 = [' H = 5,',' C2H4 = 6,', ' H2 = 7,',' H2O = 8'];

Ao = [1e17, 2e11, 3e14, 3.4e12, 1.6e13]';
Ea = [356000, 44000, 165000, 28000, 0]';
nu = [-1,2,0,0,0,0,0,0
      -1,-1,1,1,0,0,0,0
       0,0,0,-1,1,1,0,0
      -1,0,0,1,-1,0,1,0
       1,0,0,-1,-1,0,0,0];

R = 8.3144;  % Gas Constant (J/gmole-K)
p.R1 = 82.057; % Gas Constant (cc-atm/gmole-K)
p.T = 925; % Temp (K)
EXP = exp(-Ea/(R*p.T));
p.k = Ao.*EXP;
p.kp = (p.k(1)/(2*p.k(3)) + ((p.k(1)/(2*p.k(3)))^2 + ...
     ((p.k(1)*p.k(4))/(p.k(3)*p.k(5))))^0.5);
C1o = (50/760)/(82.057*p.T);  %gmole/cm3
C8o = (710/760)/(82.057*p.T);
Qf = 35.0;	%cc/sec
N1o = C1o*Qf;	%gmole/sec
N8o = C8o*Qf;
p.P = 1.0;	%atm
Initial = [N1o,0,0,0,0,0,0,N8o]';


v = [0:0.5:100]';

opts = odeset ('AbsTol', sqrt (eps), 'RelTol', sqrt (eps));
[tsolver, solution] = ode15s(@(v,x) rxrate(v,x,p),v,Initial,opts);
answer = [v solution];

Initial_s = [N1o,0,0,N8o]';

[tsolver, solution_s] = ode15s(@(v,x) rate_s(v,x,p),v,Initial_s,opts);
answer_s = [v solution_s];

temp = [v, solution, solution_s];
save -ascii ethane_comparison.dat temp;

if (~ strcmp (getenv ('OMIT_PLOTS'), 'true')) % PLOTTING
    plot (temp(:,1),[temp(:,2),temp(:,10),temp(:,7),temp(:,11)]);
    % TITLE
end % PLOTTING

rxrate.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function dNdv = rxrate(v,x,p)
    N1 = x(1);
    N2 = x(2);
    N3 = x(3);
    N4 = x(4);
    N5 = x(5);
    N6 = x(6);
    N7 = x(7);
    N8 = x(8);

    Ntot = N1 + N2 + N3 + N4 + N5 + N6 + N7 + N8;
    Ctot = p.P/(p.R1*p.T);
    C1 = (N1/Ntot)*Ctot;
    C2 = (N2/Ntot)*Ctot;
    C4 = (N4/Ntot)*Ctot;
    C5 = (N5/Ntot)*Ctot;

    r1 = p.k(1)*C1;
    r2 = p.k(2)*C1*C2;
    r3 = p.k(3)*C4;
    r4 = p.k(4)*C1*C5;
    r5 = p.k(5)*C4*C5;

    dNdv = zeros (8, 1);

    dNdv(1) = -r1 - r2 - r4 + r5;
    dNdv(2) = 2*r1 - r2;
    dNdv(3) = r2;
    dNdv(4) = r2 - r3 + r4 - r5;
    dNdv(5) = r3  - r4 - r5;
    dNdv(6) = r3;
    dNdv(7) = r4;
    dNdv(8) = 0;

rate_s.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
function dNdv = rate_s(v,x,p)
    N1 = x(1);
    N6 = x(2);
    N7 = x(3);
    N8 = x(4);

    Ntot = N1 + N6 + N7 + N8;
    Ctot = p.P/(p.R1*p.T);
    C1 = (N1/Ntot)*Ctot;
    r = p.k(3)*p.kp*C1;

    dNdv = zeros (4, 1);

    dNdv(1) = -r;
    dNdv(2) = r;
    dNdv(3) = r;
    dNdv(4) = 0;