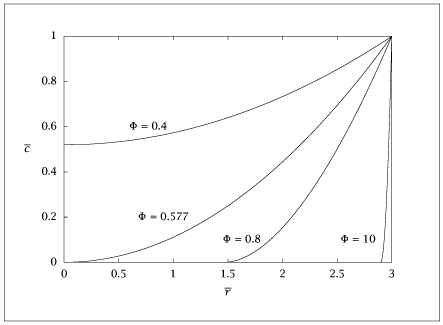
Figure 7.11:

Dimensionless concentration versus radius for zero-order reaction in a spherical pellet.

Code for Figure 7.11

Text of the GNU GPL.

main.py

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
# Converted from cvsrnsmall.m - concentration profiles for n<1 (partial saturation)
import numpy as np
from scipy.integrate import solve_ivp
from misc import octave_save

p = dict(order=0., q=2., k=2.)
thielevec = [0.4, 0.57735, 0.8, 10.]

eps_sq = np.sqrt(np.finfo(float).eps)
c0  = 0.01
der = 1e-8
start = 1.

nfine   = 200
ncoarse = 100
fine    = np.logspace(np.log10(start), np.log10(start+1), nfine)
coarse  = np.logspace(np.log10(start+2), np.log10(40.), ncoarse)
tout2   = np.concatenate([fine, coarse[1:]])

def f_ode(t, x, p):
    xdot = np.zeros(2)
    xdot[0] = x[1]
    if t == 0:
        xdot[1] = p['k'] * x[0]**p['order']
    else:
        xdot[1] = -p['q']/t * x[1] + p['k'] * x[0]**p['order']
    return xdot

def make_event(thiele, p):
    def g(t, x):
        if x[0] == 0:
            return np.inf
        val = (np.sqrt((p['order']+1)/2 * x[0]**(p['order']-1) * p['k'])
               * t / (p['q']+1))
        return val - thiele
    g.terminal  = True
    g.direction = 0
    return g

nt = len(thielevec)
table_list = []
tout_stage1 = np.concatenate([[0.], np.logspace(-2, 5, 400)])

for i in range(nt):
    thiele = thielevec[i]
    if i <= 1:
        # Stage 1: no dead zone, integrate from center outward
        x0   = np.array([c0, 0.])
        ev   = make_event(thiele, p)
        sol  = solve_ivp(lambda t, x: f_ode(t, x, p),
                         [tout_stage1[0], tout_stage1[-1]], x0,
                         method='Radau', t_eval=tout_stage1,
                         events=ev, rtol=eps_sq, atol=eps_sq)
        if sol.t_events[0].size > 0:
            t_end = sol.t_events[0][0]
            t_use = tout_stage1[tout_stage1 <= t_end]
            sol2  = solve_ivp(lambda t, x: f_ode(t, x, p),
                              [tout_stage1[0], t_end], x0,
                              method='Radau', t_eval=t_use,
                              rtol=eps_sq, atol=eps_sq)
            tsteps = sol2.t
            x      = sol2.y.T
        else:
            tsteps = sol.t
            x      = sol.y.T
        tabletmp = np.column_stack([tsteps/tsteps[-1]*(p['q']+1),
                                     x[:,0]/x[-1,0]])
    else:
        # Stage 2: dead zone exists; integrate from dead zone boundary outward.
        # Use event to identify the pellet surface (same as stage 1 logic).
        # Stage 2 starts at t=start=1 (dead zone boundary), NOT t=0,
        # because x[1]=der≠0 causes -q/t singularity at t=0.
        tout_s2 = np.concatenate([np.logspace(np.log10(start), np.log10(start+1), nfine),
                                   np.logspace(np.log10(start+2), np.log10(1e5), 600)])
        x0_s2  = np.array([der, der])
        ev_s2  = make_event(thiele, p)
        sol_ev = solve_ivp(lambda t, x: f_ode(t, x, p),
                           [tout_s2[0], tout_s2[-1]], x0_s2,
                           method='Radau', t_eval=tout_s2,
                           events=ev_s2, rtol=eps_sq, atol=eps_sq)
        if sol_ev.t_events[0].size > 0:
            t_end = sol_ev.t_events[0][0]
            t_use = np.append(tout_s2[tout_s2 < t_end], t_end)
            sol2  = solve_ivp(lambda t, x: f_ode(t, x, p),
                              [tout_s2[0], t_end], x0_s2,
                              method='Radau', t_eval=t_use,
                              rtol=eps_sq, atol=eps_sq)
            ts_live = sol2.t
            x_live  = sol2.y.T
        else:
            ts_live = sol_ev.t
            x_live  = sol_ev.y.T
            t_end   = ts_live[-1]
        # Build live-zone profile (normalized so surface = q+1)
        live_r = ts_live / t_end * (p['q']+1)
        live_c = x_live[:,0] / x_live[-1,0]
        # Prepend dead zone (c=0 from r=0 to r=r_c)
        r_c_norm = ts_live[0] / t_end * (p['q']+1)
        dead_r = np.linspace(0., r_c_norm, 20)
        dead_c = np.zeros(20)
        tabletmp = np.column_stack([np.concatenate([dead_r, live_r[1:]]),
                                    np.concatenate([dead_c, live_c[1:]])])
    table_list.append(tabletmp)

octave_save('cvsrnsmall.dat',
            *[('table%d' % i, table_list[i]) for i in range(nt)])