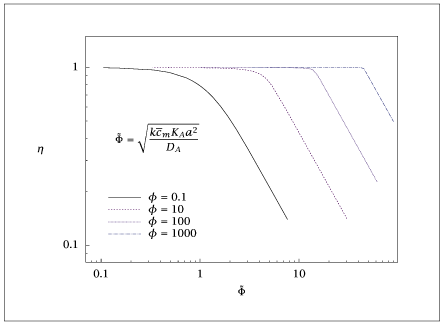
Figure 7.13:

Effectiveness factor versus an inappropriate Thiele modulus in a slab; Hougen-Watson kinetics.

Code for Figure 7.13

Text of the GNU GPL.

main.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# Converted from etahougwat.m - eta for Hougen-Watson kinetics (Langmuir-Hinshelwood)
import numpy as np
from scipy.integrate import solve_ivp
from misc import save_ascii

p1  = 1.
p2  = 1.
npts = 200
phivec = [0.1, 10., 100., 1000.]
nphi   = len(phivec)
results = None

eps_sq = np.sqrt(np.finfo(float).eps)

def hougensrt(t, x, p1, p2):
    ca    = x[0]; dcadr = x[1]; s1 = x[2]; s2 = x[3]
    return [dcadr,
            p1*p2*ca / (1 + p2*ca),
            s2,
            p1*ca/(1+p2*ca)**2 + p1*p2*s1/(1+p2*ca)**2]

def make_g(phi_target, p1, p2):
    def g(t, x):
        return p2*x[0] - phi_target
    g.terminal  = True
    g.direction = 0
    return g

for j in range(nphi):
    phi = phivec[j]
    p2vec = [1e-40, 1e-10, .1, 1., 10., 20., 30., 40., 50., 55.,
             60., 65., 70., 75., 80., 90., 95., 99., 99.5]
    if phi >= 100.:
        p2vec[0] = 1e-20
    np2 = len(p2vec)
    c0  = 1e-2 * phi
    Phivec = np.zeros(np2)
    etavec = np.zeros(np2)

    for i in range(np2):
        p2 = p2vec[i]
        rstop  = max(100., 100.*np.sqrt(1./p2))
        rsteps = np.concatenate([[0.], np.linspace(0.001, rstop, npts)])
        x0     = np.array([c0, 0., 0., 0.])
        ev     = make_g(phi, p1, p2)
        sol    = solve_ivp(lambda t, x: hougensrt(t, x, p1, p2),
                           [rsteps[0], rsteps[-1]], x0,
                           method='Radau', t_eval=rsteps,
                           events=ev, rtol=eps_sq, atol=eps_sq)
        # Use event time/state if event fired; Octave's ode15s appends event
        # point to output, but scipy solve_ivp with t_eval does not.
        if len(sol.t_events[0]) > 0:
            r1 = sol.t_events[0][0]
            xf = sol.y_events[0][0]
        else:
            r1 = sol.t[-1]
            xf = sol.y[:, -1]
        Phivec[i] = np.sqrt(p1*p2) * r1
        etavec[i] = ((1 + phi) * xf[1] * r1 / xf[0] / Phivec[i]**2)

    Phiprimevec = phi/(1+phi) / np.sqrt(2*(phi - np.log(1+phi))) * Phivec
    block = np.column_stack([Phivec, Phiprimevec, etavec])
    results = block if results is None else np.column_stack([results, block])

save_ascii('etahougwat.dat', results)