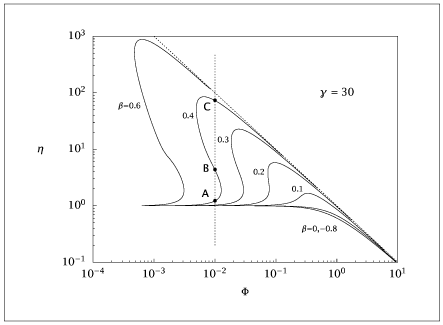
Figure 7.19:

Effectiveness factor versus normalized Thiele modulus for a first-order reaction in nonisothermal spherical pellet.

Code for Figure 7.19

Text of the GNU GPL.

main.py

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
# Converted from wh.m - Weisz-Hicks eta vs phi, parametric search (multiple beta)
import numpy as np
from scipy.optimize import fsolve
from scipy.special import exp1
from misc import colloc, octave_save

p = dict(gamma=30.)
n       = 60
npoint  = 75
betavals = [0.6, 0.4, 0.3, 0.2, 0.1, 0., -0.8]
rE0      = [0.15]*len(betavals)
rE0[4]   = 0.1
Rad      = 3.
p['cS']  = 1.

options_tol = 1e-8

R_col, A_col, B_col, Q_col = colloc(n-2, 'left', 'right')
R_col = R_col * Rad
A_col = A_col / Rad
B_col = B_col / (Rad**2)
p['R'] = R_col; p['A'] = A_col; p['B'] = B_col

def indef(x, a, b):
    # indefinite integral for calcI
    # expi(z) = -E1(-z) for z < 0; here z = -a/(b*(x-1)-1)
    z    = -a / (b*(x-1) - 1)
    expi = -(exp1(z) + np.pi*1j)
    val  = (np.exp(a) * (b*x*np.exp(a/(b*(x-1)-1)) * (a+b*x)
                          - a*(a+2*b+2)*expi)
             - (b+1)*(a+b+1)*np.exp(a*(1./(b*(x-1)-1)+1))) / (2*b**2)
    return val.real

def calcI(gam, beta):
    if beta == 0.:
        return 1.
    return np.sqrt(2*(indef(1., gam, beta) - indef(0., gam, beta)))

def eta_initial(c, p):
    phi_hat = p['phi_ini'] * p['I']
    ep = np.exp(p['gamma']*p['beta']*(1-c) / (1 + p['beta']*(1-c)))
    retval = p['A']@c * 2./p['R'] + p['B']@c - phi_hat**2 * c * ep
    retval[0]  = p['A'][0,:]@c
    retval[-1] = c[-1] - p['cS']
    return retval

def eta_calc(para, p):
    c   = para[:-1]; psi = para[-1]
    eta = 10**(p['rE']*np.sin(psi) + np.log10(p['eta_prev']))
    phi = 10**(p['rE']*np.cos(psi) + np.log10(p['phi_prev']))
    phi_hat = phi * p['I']
    ep  = np.exp(p['gamma']*p['beta']*(1-c) / (1 + p['beta']*(1-c)))
    retval = np.zeros(len(para))
    retval[:-1] = p['A']@c * 2./p['R'] + p['B']@c - phi_hat**2 * c * ep
    retval[0]   = p['A'][0,:]@c
    retval[-2]  = c[-1] - p['cS']
    dcdr   = p['A']@c
    eta_colloc = dcdr[-1] / phi_hat**2
    retval[-1]  = eta - eta_colloc
    return retval

nbeta       = len(betavals)
phistore    = [[] for _ in range(nbeta)]
etastore    = [[] for _ in range(nbeta)]
p['phi_ini'] = 5e-4
para_end     = 0.01
In01         = np.ones(n)

for j in range(nbeta):
    p['beta']     = betavals[j]
    p['I']        = calcI(p['gamma'], p['beta'])
    p['rE']       = rE0[j]
    p['phi_prev'] = p['phi_ini']
    psi_prev      = 0.; delpsi = 0.
    In0           = np.append(np.ones(n), 0.)

    for i in range(npoint):
        if i == 0:
            ini, _, info, _ = fsolve(lambda c: eta_initial(c, p), In01,
                                      full_output=True)[:4]
            deriv     = p['A']@ini
            p['eta_ini'] = deriv[-1] / (p['phi_ini']*p['I'])**2
            p['eta_prev'] = p['eta_ini']
            phistore[j].append(p['phi_ini'])
            etastore[j].append(p['eta_ini'])

        x_sol, _, info, _ = fsolve(lambda x: eta_calc(x, p), In0,
                                    full_output=True)[:4]
        psi = x_sol[-1]
        eta = 10**(p['rE']*np.sin(psi) + np.log10(p['eta_prev']))
        phi = 10**(p['rE']*np.cos(psi) + np.log10(p['phi_prev']))
        In0      = x_sol.copy()
        In0[-1] += delpsi
        phistore[j].append(phi)
        etastore[j].append(eta)
        p['phi_prev'] = phi; p['eta_prev'] = eta
        delpsi    = psi - psi_prev; psi_prev = psi
        p['rE']   = rE0[j] * (1 - abs(delpsi/np.pi))**20
        if abs(np.log10(p['eta_prev']*p['phi_prev'])) < para_end:
            break

table_list = [np.column_stack([phistore[j], etastore[j]]) for j in range(nbeta)]
xline1 = np.array([0.001, 10.])
yline1 = np.array([1000., 0.1])
xline2 = np.array([0.01, 0.01])
yline2 = np.array([0.2, 500.])
table2 = np.column_stack([xline1, yline1, xline2, yline2])

octave_save('wh.dat',
            *[('table%d' % j, table_list[j]) for j in range(nbeta)],
            ('table2', table2))