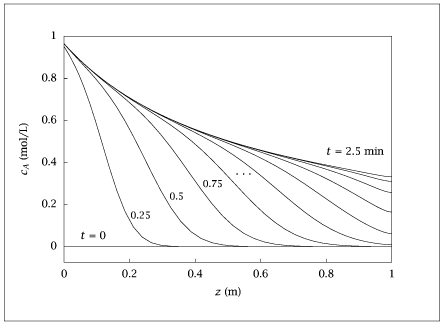
Figure 8.12:

Start-up of the tubular reactor; c_A(t,z) versus z for various times, 0\leq t\leq 2.5~min, \Delta t=0.25~min.

Code for Figure 8.12

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
% Copyright (C) 2001, James B. Rawlings and John G. Ekerdt
%
% This program is free software; you can redistribute it and/or
% modify it under the terms of the GNU General Public License as
% published by the Free Software Foundation; either version 2, or (at
% your option) any later version.
%
% This program is distributed in the hope that it will be useful, but
% WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
% General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program; see the file COPYING.  If not, write to
% the Free Software Foundation, 59 Temple Place - Suite 330, Boston,
% MA 02111-1307, USA.

%
%
% 2 A --> B,  r = k c_A^order
%
%
% transient behavior in a dispersed plug flow reactor
% steady-state profile in a PFR
% jbr, 10/20/01
%
% Revised 8/16/2018

p.k = 1/2;
p.v = 1/2;
p.D = 0.01;
p.caf = 1;
length = 1;
ncolpt = 50;
p.order = 2;
[col.z, col.A, col.B, col.Q] = colloc(ncolpt - 2,'left','right');


%x0=ones(ncolpt,1);
%[x, fval, info] = fsolve('pfrcol',x0);
%info


tsteps = linspace(0, 2.5, 11);
% initial condition, zero conc. in tube
y0 = zeros(ncolpt, 1);
ydot0 = zeros(ncolpt, 1);
[tout, y] = ode15i(@(t, y, ydot) pfrtran(t, y, ydot, ncolpt, p, col),...
                        tsteps, y0, ydot0);

table = [col.z y'];

save -ascii dispersedpfrtran.dat table;

if (~ strcmp (getenv ('OMIT_PLOTS'), 'true')) % PLOTTING
    plot (table(:,1), table(:,2:12));
    % TITLE
end % PLOTTING

pfrcol.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function res = pfrcol(x, ncolpt, p, col)
    % express the diff eq at every collocation point
    first = col.A*x;
    Ra = -2*p.k*(x.^p.order);
    second = col.B*x;
    res = -p.v*first + p.D*second + Ra;
    % write over the first and last points with the
    % boundary conditions
    res(1) = p.v*x(1) - p.D*first(1) - p.v*p.caf;
    res(ncolpt) = first(ncolpt);

pfrtran.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function res = pfrtran(t, y, ydot, ncolpt, p, col)
    tmp = pfrcol(y, ncolpt, p, col);
    a = tmp(1);
    b = tmp(ncolpt);
    res = ydot-tmp;
    %
    % put bc at ends
    %
    res(1) = a;
    res(ncolpt) = b;