Figure 9.22:

Monte Carlo evaluation of confidence intervals.

Code for Figure 9.22

Text of the GNU GPL.

main.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
%
% jbr,  4/8/18
%


model = struct;
model.transcription = 'shooting';
%model.nlp_solver_options.ipopt.linear_solver = 'ma27';
model.x = {'ca'};
model.p = {'k', 'n'};
model.d = {'m_ca'};

model.ode = @(t,x,p) {-p.k*x.ca^p.n};

model.lsq = @(t,x,p) {x.ca-x.m_ca};

tfinal = 5;
nts    = 100;
tout = linspace(0,tfinal,nts);
model.tout = tout;

pe = paresto(model);

kac   = 0.5;
ca0ac = 2;
nac   = 2.5;
thetaac = [kac; nac; ca0ac];

x_ac = ca0ac;
p_ac = [kac; nac];

y_ac = pe.simulate(0, x_ac, p_ac);

% add measurement noise
measvar = 1e-2;
measstddev = sqrt(measvar);
randn('seed',0);
noise = measstddev*randn(1,nts);

y_noisy = y_ac + noise;


% Initial guess, upper and lower bounds for the estimated parameters
small = 1e-3;
large  = 5;
np = 3;

theta0 = struct();
theta0.k = kac;
theta0.n = nac;
theta0.ca = ca0ac;

ubtheta = struct();
ubtheta.k = large;
ubtheta.n = large;
ubtheta.ca = large;

lbtheta = struct();
lbtheta.k = small;
lbtheta.n = small;
lbtheta.ca = small;


% loop here to create nmonte data sets and estimate parameters for each
%page_output_immediately(1);
%more off

nmonte = 10; % change to 500 for figure in text
alph(1:nmonte) = NaN;

for i = 1: nmonte
  %create  noisy data
  noise = measstddev*randn(1, nts);
  y_noisy = y_ac + noise;
  %estimate parameters
  [est, y, p] = pe.optimize(y_noisy, theta0, lbtheta, ubtheta);
  i
  conf = pe.confidence(est,  0.95);

  disp('Estimated parameters')
  disp(est.thetavec)
%  disp(est.theta)
%  disp('Bounding box intervals')
%  disp(conf.bbox)

  % store the estimate, contour distance of estimate from true parameters,
  % alpha value of this contour
  samplevar = est.f/(nts - np);
  thetamont(:,i) = est.thetavec;
  diff(:,i) = est.thetavec - thetaac;
  cont = diff(:,i)'*conf.H*diff(:,i)/(2*np*samplevar);
  alph(i) = fcdf(cont, np, nts-np);
end

% post processing for confidence region plot
amin = 0.0;
amax = 0.99995;
nas  = 100;
alphavec=linspace(amin,amax,nas)';
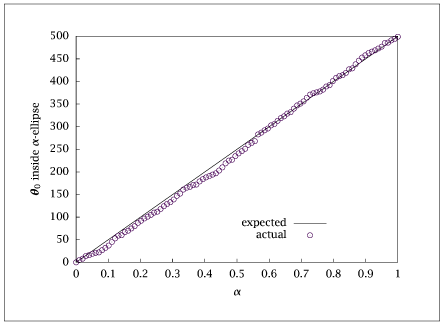
expected = alphavec*nmonte;
actual(1:nas) = NaN;
for i = 1: nas
  actual(i) = sum(alph <= alphavec(i));
end

table = [alphavec expected actual(:)];
save nthmonte.dat table;
if (~ strcmp (getenv ('OMIT_PLOTS'), 'true')) % PLOTTING
plot (alphavec, expected, alphavec, actual, '+');
% TITLE
end % PLOTTING