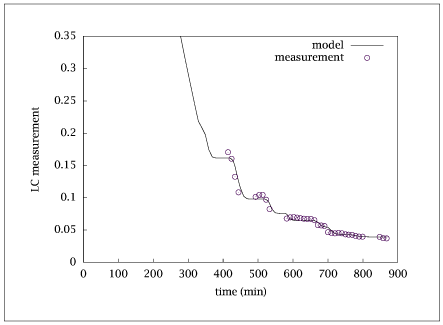
Figure 9.32

%
% We have the ODE
% dot(VR) = Qf
% dot(nA) = -k1*nA*nB/VR
% dot(nB) = Qf*cBf - nB*(k1*nA + k2*nC)/VR
% dot(nC) = nB*(k1*nA - k2*nC)/VR
% dot(nD) = k2*nC*nB/VR
%
%
% with:
% States: x = [VR, nA, nB, nC, nD]
% Qf: Volumetric flowrate of base
% cBf: Feed concentration of B
%
% Initial conditions: x(0) = [VR0, nA0, 0, 0, 0]
% Unknown parameters: k1, k2
% Output function: y = nC/(cC + 2*nD)
%
% converted bvsm.m to work with paresto.m
%
% Joel Andersson and jbr, 4/22/2018
%

% Model
% This m-file loads data file 'lc.dat'.
% This m-file loads data file 'flow.dat'.
model = struct;
model.transcription = 'shooting';
model.x = {'VR', 'nA', 'nB', 'nC', 'nD'};
model.p = {'k1', 'k2', 'cBf'};
model.nlp_solver_options.ipopt.mumps_scaling = 0;

% Dependent variables with definitions
model.y = {'lc'};
model.h = @(t, v, p) { 1 / (1 + 2*v.nD/max(v.nC, 1e-6))}; % avoid divide-by-zero

% Data and measurements
model.d = {'Qf', 'lc_m'};

% ODE right-hand-side
model.ode = @(t, v, p) {v.Qf,...
                        -p.k1*v.nA*v.nB/v.VR,...
                        v.Qf*p.cBf - v.nB*(p.k1*v.nA + p.k2*v.nC)/v.VR,...
                        v.nB*(p.k1*v.nA - p.k2*v.nC)/v.VR,...
                        p.k2*v.nC*v.nB/v.VR};

% Relative least squares objective function
model.lsq = @(t, y, p) {y.lc_m/y.lc - 1};

% Load data
teaf      = 0.00721;
teaden    = 0.728;
flow = load('flow.dat');
lc = load('lc.dat');
tQf  = [0. ; flow(:,1)];
Qf = [0. ; flow(:,2)./teaden];
tlc    = lc(:,1);
lc = lc(:,2);

% Get all time points occuring in either tlc or tflow

% Grid used in Book
% ntimes    = 200;
% tlin = linspace (0, tQf(end), ntimes)';
% [tout,~,ic] = unique([tQf; tlc; tlin]);
% Qf_ind = ic(1:numel(tQf));
% lc_ind = ic(numel(tQf)+1:numel(tQf)+numel(tlc));

% faster grid; lose a little resolution in n_B(t) plot
[tout,~,ic] = unique([tQf; tlc]);
Qf_ind = ic(1:numel(tQf));
lc_ind = ic(numel(tQf)+1:end);

% Interpolate lcmeas and Qf to this new grid
Qf = interp1(tQf, Qf, tout, 'previous');
lc_m = interp1(tlc, lc, tout, 'previous');

N = size(Qf,1);

% Replace NaNs with zeros
Qf(isnan(Qf)) = 0.;
lc_m(isnan(lc_m)) = 0.;

% Initial volume
VR0 = 2370;

% Options
model.tout = tout';
model.lsq_ind = lc_ind'; % only include lc_ind in objective

% Create a paresto instance
pe = paresto(model);

% Solution in the book
nA0 = 2.35;
k1 = 2500;
k2 = 1250;

% Options
model.tout = tout';
model.lsq_ind = lc_ind'; % only include lc_ind in objective

% Create a paresto instance
pe = paresto(model);

% Initial guess for parameters
theta0 = struct;
theta0.k1 = k1;
theta0.k2 = 0.9*k2;
theta0.cBf = teaf;

% Initial guess for initial conditions
theta0.VR = VR0;
theta0.nA = 1.1*nA0;
theta0.nB = 0;
theta0.nC = 0;
theta0.nD = 0;

% Lower bounds for parameters
lb = theta0;
lb.k1 = 0.5*theta0.k1;
lb.k2 = 0.5*theta0.k2;
lb.cBf = theta0.cBf;
lb.VR = theta0.VR;
lb.nA = 0.5*theta0.nA;
lb.nB = theta0.nB;
lb.nC = theta0.nC;
lb.nD = theta0.nD;

% Upper bounds for parameters
ub = theta0;
ub.k1 = 1.5*theta0.k1;
ub.k2 = 1.5*theta0.k2;
ub.cBf = theta0.cBf;
ub.VR = theta0.VR;
ub.nA = 1.5*theta0.nA;
ub.nB = theta0.nB;
ub.nC = theta0.nC;
ub.nD = theta0.nD;

% Estimate parameters
more off

[est,v,p] = pe.optimize([Qf'; lc_m'], theta0, lb, ub);

%est_ind = [1,2,3]; % index of estimated parameters

% Also calculate confidence intervals with 95 % confidence
conf = pe.confidence(est, 0.95);

disp('Estimated parameters')
disp(est.theta)
disp('Bounding box intervals')
disp(conf.bbox)

data = struct();
data.model = [model.tout', est.x', v.lc'];
data.measurement = [tlc, lc];
gnuplotsave('bvsm.dat', data);

if (~ strcmp (getenv ('OMIT_PLOTS'), 'true')) % PLOTTING
  clf
  subplot(2,2,1)
  hold on
  plot(model.tout, v.nA)
  plot(model.tout, v.nC)
  plot(model.tout, v.nD)
  legend({'n_A', 'n_C', 'n_D'});
  xlabel('time (min)')
  ylabel('Amount of substance (kmol)')
  title('Amount of substance of species A, C and D versus time')

  subplot(2,2,2)
  hold on
  plot(model.tout, v.nB)
  legend({'n_B'});
  xlabel('time (min)')
  ylabel('Amount of substance (kmol)')
  title('Amount of substance of species B versus time')

  subplot(2,2,3)
  stairs(model.tout, v.Qf)
  xlabel('time (min)')
  ylabel('flowrate (kg/min)')
  title('Base addition rnate')

  subplot(2,2,4)
  hold on
  plot(model.tout, v.lc)
  plot(tlc, lc, 'o')
  ylim([0, 2*max(lc)])
  legend({'model', 'measurement'});
  xlabel('time (min)')
  title('LC measurement')
end % PLOTTING
Figure 9.32:

Comparison of data to model with optimal parameters.

Code for Figure 9.32

main.m

lc.dat

flow.dat
