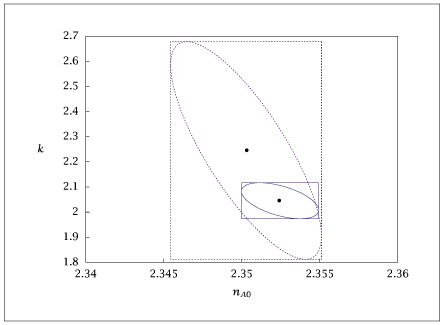
Figure 9.37

%
% We have the reduced ODE model
% dot(VR) = Qf
% dot(eps2) = Qf*cBf/(1 + k (nA0-nBadded+eps2)/(nBadded-2*eps2))
%
%
% with:
% States: x = [VR, eps2]  volume and extent of 2nd reaction
% Qf: Volumetric flowrate of base
% cBf: Feed concentration of B
%
% Initial conditions: x(0) = [VR0, 0]
% Unknown parameters: k (= k1/k2), n_A0
% Output function: y = nC/(nC + 2*nD) = 1/(1+2*nD/nC)
%
% jbr, Joel Andersson, 4/18/2018
%

% Model
% This m-file loads data file 'lc.dat'.
% This m-file loads data file 'flow.dat'.
% This m-file loads data file 'lcsim.dat'.
model = struct;
model.transcription = 'shooting';
%model.nlp_solver_options.ipopt.linear_solver = 'ma27';
model.nlp_solver_options.ipopt.mumps_scaling = 0;
% set eps to zero for algebraic model
model.nlp_solver_options.sens_linsol_options.eps = 0;
model.x = {'VR', 'eps2'};
model.p = {'nA0', 'k', 'cBf', 'VR0'};

% Dependent variables with definitions
model.y = {'lc'};


model.h = @lcmeas;

% Data and measurements
model.d = {'Qf', 'lc_m'};


% ODE right-hand-side
model.ode = @reduced_model;

% Relative least squares objective function
model.lsq = @(t, y, p) {y.lc_m/y.lc - 1};

% Load data
teaf      = 0.00721;
teaden    = 0.728;
flow = load('flow.dat');
lc = load('lc.dat');
tQf  = [0. ; flow(:,1)];
Qf = [0. ; flow(:,2)./teaden];
tlc    = lc(:,1);
lc = lc(:,2);

% Get all time points occuring in either tlc or tflow

% Grid used in Book
% ntimes    = 200;
% tlin = linspace (0, tQf(end), ntimes)';
% [tout,~,ic] = unique([tQf; tlc; tlin]);
% Qf_ind = ic(1:numel(tQf));
% lc_ind = ic(numel(tQf)+1:numel(tQf)+numel(tlc));

% faster grid; lose a little resolution in n_B(t) plot
[tout,~,ic] = unique([tQf; tlc]);
Qf_ind = ic(1:numel(tQf));
lc_ind = ic(numel(tQf)+1:end);

% Interpolate lcmeas and Qf to this new grid
Qf = interp1(tQf, Qf, tout, 'previous');
lc_m = interp1(tlc, lc, tout, 'previous');

N = size(Qf,1);

% Replace NaNs with zeros
Qf(isnan(Qf)) = 0.;
lc_m(isnan(lc_m)) = 0.;

% Initial volume
VR0 = 2370;
% "optimal" values
vrdiclo     =  2.3497;
k1k2ratio   =  2;

% Options
model.tout = tout';
model.lsq_ind = lc_ind'; % only include lc_ind in objective

% Create a paresto instance
pe = paresto(model);

% Initial guess for parameters
theta0 = struct;
theta0.nA0 = vrdiclo;
theta0.k = k1k2ratio;
theta0.cBf = teaf;
theta0.VR0 = VR0;
% Initial guess for initial conditions
theta0.VR = VR0;
theta0.eps2 = 0;

% Lower bounds for parameters
% We aren't estimating cBf and VR0
lb = theta0;
lb.nA0 = 0.5*theta0.nA0;
lb.k = 0.5*theta0.k;
lb.VR0 = theta0.VR0;
lb.cBf = theta0.cBf;
lb.VR = theta0.VR;
lb.eps2 = theta0.eps2;


% Upper bounds for parameters
ub = theta0;
ub.nA0 = 1.5*theta0.nA0;
ub.k = 1.5*theta0.k;
ub.VR0 = theta0.VR0;
ub.cBf = theta0.cBf;
ub.VR = theta0.VR;
ub.eps2 = theta0.eps2;


% Estimate parameters

[est, v, p] = pe.optimize([Qf'; lc_m'], theta0, lb, ub);

% Also calculate confidence intervals with 95 % confidence
conf = pe.confidence(est, 0.95);

disp('Estimated parameters')
disp(est.theta)
disp('Bounding box intervals')
disp(conf.bbox)

np = numel(est.conf_ind);
ndata = length(tlc);
alpha = 0.95;
Fstat = np*finv(alpha,np,ndata-np);
a     = 2*est.f/(ndata-np)*Fstat;
[xx, yy, major, minor, bbox] = ellipse (conf.H, a, 100, [est.theta.nA0; est.theta.k]);
tmp = [xx, yy];

table1 = [model.tout', v.lc'];
table2 = [tlc, lc];


% Estimate parameters again with the early time LC data

%
% Simulated the lc measurement from the beginning of the experiment.
% These data were saved by hand in lcsim.dat with
% k1k2ratio=2, vrdiclo=2.3497;
% 2nd column is without noise, 3rd column is with noise.
%
% prepend simulated data
%

flow = load('flow.dat');
lc = load('lc.dat');
lcsim = load('lcsim.dat');


tQf  = [0. ; flow(:,1)];
Qf = [0. ; flow(:,2)./teaden];
tlc = [lcsim(:,1); lc(:,1)];
lc = [lcsim(:,3); lc(:,2)];

% Get all time points occuring in either tlc or tflow

% Grid used in Book
% ntimes    = 200;
% tlin = linspace (0, tQf(end), ntimes)';
% [tout,~,ic] = unique([tQf; tlc; tlin]);
% Qf_ind = ic(1:numel(tQf));
% lc_ind = ic(numel(tQf)+1:numel(tQf)+numel(tlc));

% faster grid; lose a little resolution in n_B(t) plot
[tout,~,ic] = unique([tQf; tlc]);
Qf_ind = ic(1:numel(tQf));
lc_ind = ic(numel(tQf)+1:end);

% Interpolate lcmeas and Qf to this new grid
Qf = interp1(tQf, Qf, tout, 'previous');
lc_m = interp1(tlc, lc, tout, 'previous');

N = size(Qf,1);

% Replace NaNs with zeros
Qf(isnan(Qf)) = 0.;
lc_m(isnan(lc_m)) = 0.;

% Initial volume
VR0 = 2370;
% optimal values
vrdiclo     =  2.3497;
k1k2ratio   =  2;

% Options
model.tout = tout';
model.lsq_ind = lc_ind'; % only include lc_ind in objective

% Create a paresto instance
pesim = paresto(model);

% Lower bounds for parameters
lb = theta0;
lb.nA0 = 0.5*theta0.nA0;
lb.k = 0.5*theta0.k;
% We aren't estimating cBf and VR0
lb.VR = [theta0.VR, -inf(1,N-1)]; %zeros(1,N-1)];
lb.eps2 = [theta0.eps2, -inf(1,N-1)]; %zeros(1,N-1)];


% Upper bounds for parameters
ub = theta0;
ub.nA0 = 1.5*theta0.nA0;
ub.k = 1.5*theta0.k;

ub.VR = [theta0.VR, inf(1,N-1)];
ub.eps2 = [theta0.eps2, inf(1,N-1)];

% Estimate parameters

[estsim, v, p] = pesim.optimize([Qf'; lc_m'], theta0, lb, ub);

% Also calculate confidence intervals with 95 % confidence
confsim = pesim.confidence(estsim, 0.95);

disp('Estimated parameters')
disp(estsim.theta)
disp('Bounding box intervals')
disp(confsim.bbox)

% compute the rest of the states from the reduced model

Badded = (v.VR - p.VR0)*p.cBf;
nD = v.eps2;
nC = Badded - 2*nD;
nB = zeros(size(Badded));
eps1 = Badded-v.eps2;
nA = p.nA0 - Badded + v.eps2;
deps2dt = v.Qf*p.cBf / (1. + p.k*(p.nA0 - Badded + v.eps2)/(Badded - 2*v.eps2));

ndata = length(tlc);
Fstat = np*finv(alpha, np, ndata-np);
a     = 2*estsim.f/(ndata-np)*Fstat;
[xxex, yyex, major, minor, bboxex] = ...
   ellipse (confsim.H, a, 100, [estsim.theta.nA0; estsim.theta.k]);
tmpex = [xxex, yyex];

table1ex = [model.tout', v.lc'];
table2ex = [tlc, lc];

if (~ strcmp (getenv ('OMIT_PLOTS'), 'true')) % PLOTTING
subplot(2,2,1)
hold on
plot(model.tout, nA)
plot(model.tout, nC)
plot(model.tout, nD)
legend({'n_A', 'n_C', 'n_D'});
xlabel('time (min)')
ylabel('Amount of substance (kmol)')
title('Amount of substance of species A, C and D versus time')

subplot(2,2,2)
hold on
plot(model.tout, nB)
legend({'n_B'});
xlabel('time (min)')
ylabel('Amount of substance (kmol)')
title('Amount of substance of species B versus time')

subplot(2,2,3)
stairs(model.tout, v.Qf)
xlabel('time (min)')
ylabel('flowrate (kg/min)')
title('Base addition rate')

subplot(2,2,4)
hold on
plot(model.tout, v.lc, tlc, lc, 'o')
%ylim([0, 2*max(lc)])
legend({'model', 'measurement'});
xlabel('time (min)')
title('LC measurement')

figure()
plot(xx, yy, bbox(:,1), bbox(:,2), est.theta.nA0, est.theta.k, 'x', ...
     xxex, yyex, bboxex(:,1), bboxex(:,2), estsim.theta.nA0, estsim.theta.k, 'o')

end % PLOTTING

save bvsm_red.dat table1 table2 bbox tmp table1ex table2ex bboxex tmpex;
Figure 9.37:

Confidence intervals for reduced model without (dashed) and with (solid) redesigned experiment.

Code for Figure 9.37

main.m

lc.dat

flow.dat

lcsim.dat

lcmeas.m

reduced_model.m
