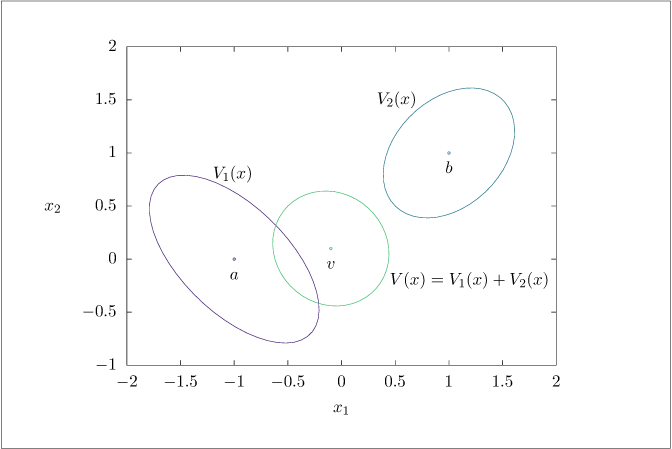
Figure 1.4:

Two quadratic functions and their sum.

Code for Figure 1.4

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
% Example sum of two quadratic functions.

a = [-1; 0];
b = [1; 1];
A = [1.25000, 0.75000; 0.75000  1.25000];
B = [1.50000, -0.50000; -0.50000, 1.50000];

% add the two quadratics
H = A + B;
h = H\(A*a + B*b);
d = -(A*a + B*b)'*h + a'*A*a + b'*B*b;

% plot resulting ellipse for combining two ellipses
% V(x) = V_1(x) + V_2(x)
level = 0.5;
npts = 50;
[xA, yA] = ellipse(A, level, npts, a);

[xB, yB] = ellipse(B, level, npts, b);

level = (2 - d/2)*2;
[xH, yH] = ellipse(H, level, npts, h);


% Make plot.
plot(xA, yA, '-r', a(1), a(2), 'or', ...
     xB, yB, '-g', b(1), b(2), 'og', ...
     xH, yH, '-b', h(1), h(2), 'ob');
legend('A', 'a', 'B', 'b', 'H = A + B', 'h', 'Location', 'NorthWest');

% Save data.
data = struct();
data.contours = [xA, yA, xB, yB, xH, yH];
data.centers = [a', b', h'];
gnuplotsave('nestedV.dat', data);

ellipse.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
% Copyright (C) 2001, James B. Rawlings and John W. Eaton
%
% This program is free software; you can redistribute it and/or
% modify it under the terms of the GNU General Public License as
% published by the Free Software Foundation; either version 2, or (at
% your option) any later version.
%
% This program is distributed in the hope that it will be useful, but
% WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
% General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program; see the file COPYING.  If not, write to
% the Free Software Foundation, 59 Temple Place - Suite 330, Boston,
% MA 02111-1307, USA.

% [x, y, major, minor, bbox] = ellipse (amat, level, n, shift)
%
% Given a 2x2 matrix, generate ellipse data for plotting.  The
% arguments N and SHIFT are optional.  If N is an empty matrix, a
% default value of 100 is used.

function [x, y, major, minor, bbox] = ellipse (amat, level, n, shift)

  if (nargin < 3)
    n = 100;
  end

  if (isempty (n))
    n = 100;
  end

  if (nargin < 4)
    shift = [0, 0];
  end

  ss = size (shift);

  if (any (ss ~= [1, 2]))
    if (ss == [2, 1])
      shift = shift';
    else
      error ('shift must be a 2-element row vector');
    end
  end

  if (nargin > 1)

    [v, l] = eig (amat / level);

    dl = diag(l);
    if (any (imag (dl)) || any (dl <= 0))
      error ('ellipse: amat must be positive definite');
    end

    % Generate contour data.

    a = 1 / sqrt (l(1,1));
    b = 1 / sqrt (l(2,2));

    t = linspace (0, 2*pi, n)';

    xt = a * cos (t);
    yt = b * sin (t);

    % Rotate the contours.

    ra = atan2 (v(2,1), v(1,1));

    cos_ra = cos (ra);
    sin_ra = sin (ra);

    x = xt * cos_ra - yt * sin_ra + shift(1);
    y = xt * sin_ra + yt * cos_ra + shift(2);

    % Endpoints of the major and minor axes.

    minor = (v * diag ([a, b]))';
    major = minor;

    major(2,:) = -major(1,:);
    minor(1,:) = -minor(2,:);

    t = [1; 1] * shift;

    major = major + t;
    minor = minor + t;

    % Bounding box for the ellipse using magic formula.

    ainv = inv (amat);
    xbox = sqrt (level * ainv(1,1));
    ybox = sqrt (level * ainv(2,2));

    bbox = [xbox ybox; xbox -ybox; -xbox -ybox; -xbox ybox; xbox ybox];

    t = [1; 1; 1; 1; 1] * shift;
    bbox = bbox + t;

  else
    error ('usage: ellipse (amat, level, n, shift)');
  end

% end%function