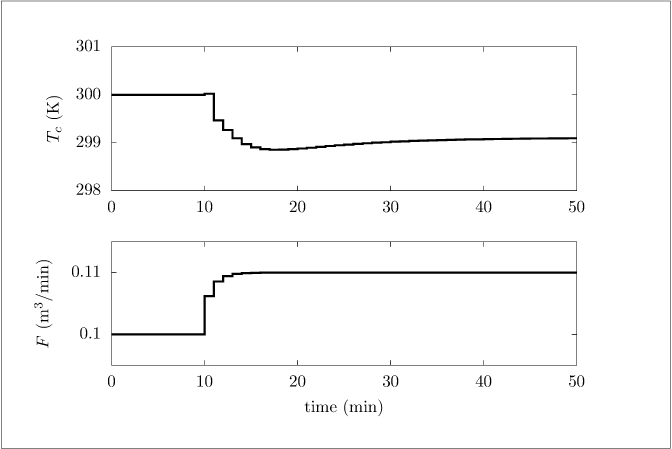
Figure 1.9:
Two manipulated inputs versus time after a step change in inlet flowrate at 10 minutes; n_d=2.
Code for Figure 1.9
Text of the GNU GPL.
main.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201 | % Applies offset-free linear MPC to the nonlinear CSTR.
% See Pannocchia and Rawlings, AIChE J, 2002.
mpc = import_mpctools();
% Parameters and sizes for the nonlinear system
Delta = 1;
Nx = 3;
Nu = 2;
Ny = Nx;
Np = 1;
small = 1e-5; % Small number.
% Parameters.
pars = struct();
pars.T0 = 350; % K
pars.c0 = 1; % kmol/m^3
pars.r = 0.219; % m
pars.k0 = 7.2e10; % min^-1
pars.E = 8750; % K
pars.U = 54.94; % kJ/(min m^2 K)
pars.rho = 1e3; % kg/m^3
pars.Cp = 0.239; % kJ/(kg K)
pars.DeltaH = -5e4; % kJ/kmol
pars.A = pi()*pars.r.^2;
pars.rhoCp = pars.rho*pars.Cp;
ode = @(x, u, p) cstrode(x, u, p, pars);
ode_casadi = mpc.getCasadiFunc(ode, [Nx, Nu, Np], ...
{'x', 'u', 'p'}, {'ode'});
cstrsim = mpc.getCasadiIntegrator(ode, Delta, [Nx, Nu, Np], ...
{'x', 'u', 'p'}, {'cstr'});
% Steady-state values.
cs = 0.878; % kmol/m^3
Ts = 324.5; % K
hs = 0.659; % m
Fs = 0.1; % m^3/min
Tcs = 300; % K
F0s = 0.1; % m^3/min
xs = [cs; Ts; hs];
us = [Tcs; Fs];
ps = [F0s];
CVs = [1, 3]; % Control Concentration and height.
% Simulate a few steps so we actually get dx/dt = 0 at steady state.
for i = 1:10
xs = full(cstrsim(xs, us, ps));
end
cs = xs(1);
Ts = xs(2);
hs = xs(3);
% Get linearized model and linear controller.
model = mpc.getLinearizedModel(ode_casadi, {xs, us, ps}, ...
{'A', 'B', 'Bp'}, Delta);
A = model.A;
B = model.B;
C = eye(Ny);
Bp = model.Bp;
Q = diag(1./xs.^2);
R = diag(1./us.^2);
K = -dlqr(A, B, Q, R);
% Pick whether to use good disturbance model.
disturbancemodels = {'Good', 'Offset', 'Undetectable', 'No'};
data = struct();
for dmodel = 1:length(disturbancemodels)
dmodel = disturbancemodels{dmodel};
fprintf('Choosing %s disturbance model.\n', dmodel);
switch dmodel
case 'Good'
% disturbance model 6; no offset
Nd = 3;
Bd = zeros(Nx, Nd);
Bd(:,3) = B(:,2);
Cd = [1 0 0; 0 0 0; 0 1 0];
case 'Offset'
% disturbance model with offset
Nd = 2;
Bd = zeros(Nx, Nd);
Cd = [1 0; 0 0; 0 1];
case 'Undetectable'
Nd = 3;
Bd = zeros(Nx, Nd);
Cd = eye(Ny, Nd);
case 'No'
Nd = 0;
Bd = zeros(Nx, Nd);
Cd = zeros(Ny, Nd);
otherwise
error('Unknown choice for disturbance model: %s', dmodel);
end
Aaug = [A, Bd; zeros(Nd, Nx), eye(Nd)];
Baug = [B; zeros(Nd, Nu)];
Caug = [C, Cd];
Naug = size(Aaug,1);
% Detectability test of disturbance model
detec = rank([eye(Naug) - Aaug; Caug]);
if detec < Nx + Nd
fprintf(' * Augmented system is not detectable!\n')
break
end
% Set up state estimator; use KF
Qw = zeros(Naug);
Qw(1:Nx,1:Nx) = small*eye(Nx);
Qw(Nx+1:end,Nx+1:end) = small*eye(Nd);
Qw(end,end) = 1.0;
Rv = small*diag(xs.^2);
[L, ~, Pe] = dlqe(Aaug, eye(Naug), Caug, Qw, Rv);
Lx = L(1:Nx,:);
Ld = L(Nx+1:end,:);
% Closed-loop simulation.
Nsim = 50;
x = NaN(Nx, Nsim + 1);
x(:, 1) = 0;
y = NaN(Ny, Nsim + 1);
u = NaN(Nu, Nsim);
randn('seed', 927);
v = zeros(Ny, Nsim + 1);
xhatm = NaN(Nx, Nsim + 1);
xhatm(:,1) = 0;
dhatm = NaN(Nd, Nsim + 1);
dhatm(:,1) = 0;
xhat = NaN(Nx, Nsim);
dhat = NaN(Nd, Nsim);
xtarg = zeros(Nx, Nsim);
utarg = zeros(Nu, Nsim);
% Disturbance and setpoint.
p = zeros(Np, Nsim);
p(10:end) = 0.1*F0s;
ysp = zeros(Ny, Nsim);
% Steady-state target matrices.
if length(CVs) > Nu
error('At most 2 CVs can be specified!');
end
H = full(sparse(1:length(CVs), CVs, 1, length(CVs), Ny));
Ginv = [eye(Nx) - A, -B; H*C, zeros(size(H,1), Nu)]\eye(Nx + Nu);
% Start loop.
for i = 1:(Nsim + 1)
% Take measurement.
y(:,i) = C*x(:,i) + v(:,i);
% Advance state measurement.
e = y(:,i) - C*xhatm(:,i) - Cd*dhatm(:,i);
xhat(:,i) = xhatm(:,i) + Lx*e;
dhat(:,i) = dhatm(:,i) + Ld*e;
% Stop if at last time.
if i == Nsim + 1
break
end
% Use steady-state target selector.
targ = Ginv*[Bd*dhat(:,i); H*(ysp(:,i) - Cd*dhat(:,i))];
xtarg(:,i) = targ(1:Nx);
utarg(:,i) = targ((Nx + 1):end);
% Apply control law.
u(:,i) = K*(xhat(:,i) - xtarg(:,i)) + utarg(:,i);
% Evolve plant. Our variables are deviation but cstrsim needs positional.
x(:,i + 1) = full(cstrsim(x(:,i) + xs, u(:,i) + us, p(:,i) + ps)) - xs;
% advance state estimates
xhatm(:,i + 1) = A*xhat(:,i) + B*u(:,i) + Bd*dhat(:,i);
dhatm(:,i + 1) = dhat(:,i);
end
% Convert to positional units.
u = bsxfun(@plus, u, us);
x = bsxfun(@plus, x, xs);
ysp = bsxfun(@plus, ysp, C*xs);
ysp(setdiff(1:Ny, CVs),:) = NaN(); % Mask out uncontrolled variables.
% Make a plot.
mpc.mpcplot('x', x, 'u', u, 'xsp', ysp, 'xnames', {'c', 'T', 'h'}, ...
'unames', {'T_c', 'F'}, 'spcolor', 'r', ...
'title', sprintf('%s Disturbance Model', dmodel));
% Store data.
u = [u, u(:,end)]; % Duplicate final point.
data.(dmodel) = struct('x', [0:Nsim; x]', 'u', [0:Nsim; u]');
end
% Save data.
gnuplotsave('cstr.dat', data);
|
cstrode.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | function rhs = cstrode(x, u, p, pars)
% Nonlinear ODE model for reactor.
c = x(1);
T = x(2);
h = x(3) + eps(); % Avoids division by zero.
Tc = u(1);
F = u(2);
F0 = p(1);
k = pars.k0*exp(-pars.E/T);
rate = k*c;
dcdt = F0*(pars.c0 - c)/(pars.A*h) - rate;
dTdt = F0*(pars.T0 - T)/(pars.A*h) ...
- pars.DeltaH/pars.rhoCp*rate ...
+ 2*pars.U/(pars.r*pars.rhoCp)*(Tc - T);
dhdt = (F0 - F)/pars.A;
rhs = [dcdt; dTdt; dhdt];
|
