Figure 2.1:

Example of MPC.

Code for Figure 2.1

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
%
% compute simple LQ MPC solution
% jbr, 8/13/2008
%
global H uub ulb
A = 1;
B = 1;
Q = 1;
R = 1;
N = 2;

H = [3, 1; 1, 2];
uub = ones(N,1);
ulb = -uub;

T = 15;



% closed-loop simulation

x0 = 10;
x = zeros(1,T+1);
x(:,1) = x0;
u = zeros(1,T+1);
time = [0:T];
for k = 1:T+1
  u(:,k) = control_law(x(:,k));
  if k == T + 1
    break
  end
  x(:,k+1) = A*x(:,k) + B*u(:,k);
end


% evaluate control law

xmin = -3;
xmax = -xmin;
nxs = 100;
xvec = linspace(xmin, xmax, nxs)';

for i = 1:nxs
  uvec(i) = control_law(xvec(i));
end
uvec = uvec(:);

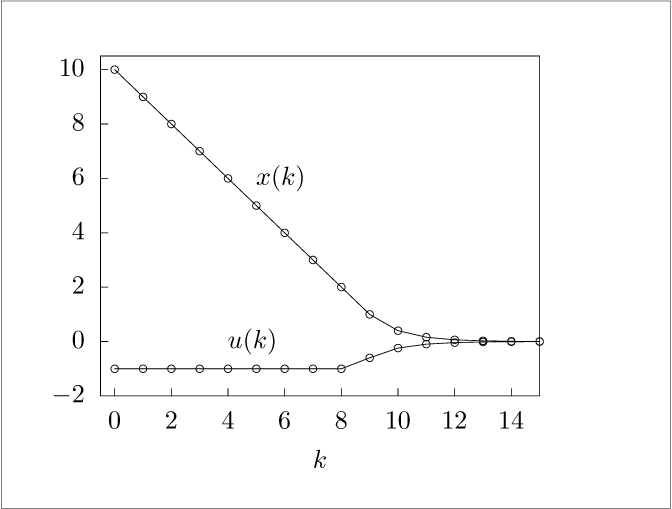
figure(1);
plot(time, [x; u], '-o')
axis([0,T,-2,10]);

figure(2);
plot(xvec,uvec)
axis([xmin, xmax, 2*ulb(1), 2*uub(1)]);

data1 = [time', x',  u'];
data2 = [xvec, uvec];
save('lqmpc.dat', 'data1', 'data2');

control_law.m

1
2
3
4
5
6
function u = control_law(x)
  global H uub ulb
  uN = - inv(H)*[2;1]*x;
  uN = min(uN, uub);
  uN = max(uN, ulb);
  u = uN(1);