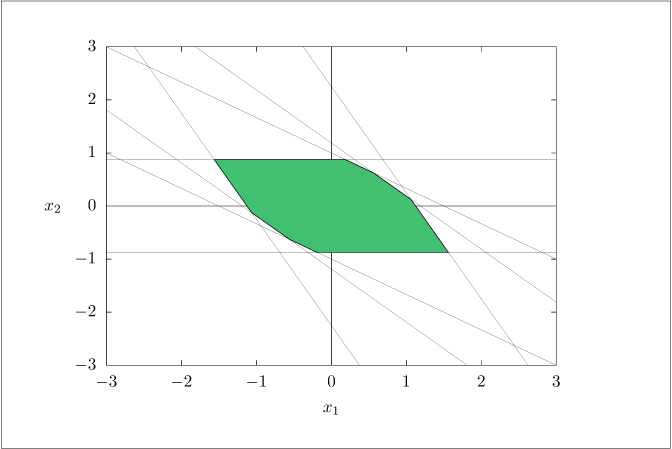
Figure 2.10:
Region of attraction (shaded region) for constrained MPC controller of Exercise \ref {exer:Xnterminal}.
Code for Figure 2.10
Text of the GNU GPL.
main.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | % Exercise "Terminal constraint and region of attraction" part (c)
% Define model, cost function, and bounds.
A = [2, 1; 0, 2];
B = [1, 0; 0, 1];
N = 3;
alpha = 1e-5;
Q = alpha*eye(2);
R = eye(2);
K = zeros(size(B')); % Don't actually use this, but it's needed for findXn().
% Bounds.
xlb = [-inf(); -inf()];
xub = [5; inf()];
ulb = [-1; -1];
uub = [1; 1];
% Find region of stability.
[Xn, V, Z] = findXn(A, B, K, N, xlb, xub, ulb, uub, 'termeq');
% Compute lines.
p = V{end}; % Vertices of Xn.
xlims = [-3, 3];
ylims = [-3, 3];
Xnlines = vertices2lines(p, xlims, ylims);
% Save data files.
p = p'; % Vertices of Xn. 'Xnterminal_c.dat'
l = Xnlines; % Lines for all sides. 'Xnterminal_lines_c.dat'
save('Xnterminal_c.dat', 'p', 'l');
|
findXn.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84 | function [Xn, V, Z] = findXn(A, B, K, N, xlb, xub, ulb, uub, terminal, doplot)
% [Xn, V, Z] = findXn(A, B, K, N, xlb, xub, ulb, uub, terminal, [doplot])
%
% Calculates the various sets for the given system and parameters.
%
% Most inputs are self-explanatory. terminal should be either the string
% 'termeq' to use a terminal equality constraint, or 'lqr' to use the
% maximum LQR-invariant set.
%
% Output Xn is a cell array defining each of the \bbX_n sets. Xn{1} is the
% terminal set, Xn{2} is \bbX_1, etc. V is a cell array with each entry giving
% the extreme vertices of the corresponding Xn (as a 2 by N matrix). Z is a
% structure defining the feasible space.
%
% Also makes a plot of all the sets unless doplot is False.
narginchk(9, 10);
if nargin() < 10
doplot = true();
end
% Define constraints for Z.
Nx = size(A, 1);
[Az, bz] = hyperrectangle([xlb; ulb], [xub; uub]);
Z = struct('G', Az(:,1:Nx), 'H', Az(:,(Nx + 1):end), 'psi', bz);
% Decide terminal constraint.
switch terminal
case 'termeq'
% Equality constraint at the origin.
Xf = [0; 0];
case 'lqr'
% Build feasible region considering x \in X and Kx \in U.
[A_U, b_U] = hyperrectangle(ulb, uub);
A_lqr = A_U*K;
b_lqr = b_U;
[A_X, b_X] = hyperrectangle(xlb, xub);
Acon = [A_lqr; A_X];
bcon = [b_lqr; b_X];
% Use LQR-invariant set.
Xf = struct();
ApBK = A + B*K; % LQR evolution matrix.
[Xf.A, Xf.b] = calcOinf(ApBK, Acon, bcon);
[~, Xf.A, Xf.b] = removeredundantcon(Xf.A, Xf.b);
otherwise
error('Unknown value for terminal: %s', terminal);
end
% Now do feasible sets computation.
if doplot
figure();
hold('on');
colors = jet(N + 1);
end
Xn = cell(N + 1, 1);
Xn{1} = Xf;
names = cell(N + 1, 1);
names{1} = 'Xf';
V = cell(N + 1, 1);
for n = 1:(N + 1)
% Plot current set.
if n > 1
names{n} = sprintf('X%d', n - 1);
end
if doplot
plotargs = {'-o', 'color', colors(n,:)};
else
plotargs = {false()};
end
V{n} = plotpoly(Xn{n}, plotargs{:});
if n == (N + 1)
break
end
% Compute next set. Also need to prune constraints.
nextXn = computeX1(Z, A, B, Xn{n});
[~, nextXn.A, nextXn.b] = removeredundantcon(nextXn.A, nextXn.b);
Xn{n + 1} = nextXn;
end
if doplot
legend(names{:});
end
end%function
|
hyperrectangle.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function [A, b] = hyperrectangle(lb, ub)
% [A, b] = hyperrectangle(lb, ub)
%
% Returns halfspace representation of hyperrectangle with bounds lb and ub.
% Any infinite or NaN bounds are ignored.
narginchk(2, 2);
if ~isvector(lb) || ~isvector(ub) || length(lb) ~= length(ub)
error('Inputs must be vectors of the same size!');
end
A = kron(eye(length(lb)), [1; -1]);
b = reshape([ub(:)'; -lb(:)'], 2*length(lb), 1);
goodrows = ~isinf(b) & ~isnan(b);
A = A(goodrows,:);
b = b(goodrows);
end%function
|
calcOinf.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93 | function [AOinf, bOinf, tstar] = calcOinf(F, A, b, tmax)
% [AOinf, bOinf, tstar] = calcOinf(F, A, b, [tmax])
%
% Calculates the maximum admissible set for x^+ = F*x subject to A*x <= b. Note
% that if F is unstable, this procedure will not work.
%
% tmax is the value of t to stop at, as an upper bound is not known a-priori.
% The default value is 100. If this bound is reached without termination, then
% tstar is set to inf.
% Arguments and sizes.
narginchk(3, 4);
if nargin() < 4
tmax = 100;
end
Nx = size(F, 1);
if size(F, 2) ~= Nx
error('F must be square!');
end
Nc = size(A, 1);
if size(A, 2) ~= Nx
error('A must have the same number of columns as F!');
elseif ~isvector(b) || length(b) ~= Nc
error('b must be a vector with an entry for each row of A!');
end
b = b(:);
% Define linear programming function.
if isOctave()
solvelp = @solvelp_octave;
else
solvelp = @solvelp_matlab;
end
% Start the algorithm.
Ft = eye(Nx);
AOinf = zeros(0, Nx);
bOinf = zeros(0, 1);
tstar = inf();
for t = 0:tmax
% Add constraints for new time point.
AOinf = [AOinf; A*Ft];
bOinf = [bOinf; b];
% Recalculate objective.
Ft = F*Ft;
fobj = A*Ft;
% Maximize each component, stopping early if any bounds are violated.
okay = true();
for i = 1:Nc
[obj, feas] = solvelp(fobj(i,:), AOinf, bOinf);
if ~feas || obj > b(i)
okay = false(); % N isn't high enough Need to keep going.
continue
end
end
% If everything was feasible, then we're done.
if okay
tstar = t;
break
end
end
end%function
function [obj, feas] = solvelp_octave(f, A, b)
% Octave version to solve LP.
Nx = size(A, 2);
lb = -inf(Nx, 1);
ub = inf(Nx, 1);
ctype = repmat('U', size(A, 1), 1);
vtype = repmat('C', Nx, 1);
sense = -1; % Maximization.
[~, obj, err, extra] = glpk(f, A, b, lb, ub, ctype, vtype, sense, ...
struct('msglev', 0));
status = extra.status;
feas = (err == 0) && (status == 5);
end%function
function [obj, feas] = solvelp_matlab(f, A, b)
% Matlab version to solve LP.
prob = struct('f', -f, 'Aineq', A, 'bineq', b, 'options', ...
optimoptions('linprog', 'Algorithm', 'dual-simplex', ...
'display', 'off'), 'solver', 'linprog');
[~, obj, exitflag] = linprog(prob);
obj = -obj; % Fix sign of objective value.
feas = (exitflag == 1);
end%function
|
removeredundantcon.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107 | function [nr, Anr, bnr, h, x0] = removeredundantcon(A, b, x0, tol, qhullopts)
% [nr, Anr, bnr, h, x0] = removeredundantcon(A, b, [x0], [tol], qhullopts)
%
% Finds the non-redundant constraints for the polyhedron Ax <= b. nr is a
% column vector with the non-redundant rows. If requested, Anr and bnr are the
% non-redundant parts of A and b.
%
% If x0 is supplied, it must be in the strict interior of A. Otherwise an error
% is thrown. Specifying a valid x0 will speed up the function.
%
% tol is used to decide how much on the interior we need to be. If not supplied,
% the default value is 1e-8*max(1, norm(b)/N). Note that this may be too large
% if b is poorly scaled.
%
% qhullopts is a string of options to pass to qhull. Defaults are described in
% the documentation for convhulln (see `help convhulln`).
%
% h is the output of convhulln, which actually describes the facets, and x0
% is a point on the interior of the polyhedron. Note that if the input
% polyhedron is unbounded, h may have zeros in some entries corresponding to the
% row of all zeros that needs to be added for the method to work.
%
% Note that this requires finding convex hull in N + 1 dimensions, where N
% is the number of columns of A. Thus, this will get very slow if A has a lot
% of columns.
narginchk(2, 5);
% Force b to column vector and check sizes.
b = b(:);
if isrow(b)
b = b';
end
if size(A, 1) ~= length(b)
error('A and b must have the same number of rows!');
end
if nargin() < 3
x0 = [];
end
if nargin() < 4 || isempty(tol)
tol = 1e-8*max(1, norm(b)/length(b));
elseif tol <= 0
error('tol must be strictly positive!')
end
if nargin() < 5
if size(A, 2) <= 4
qhullopts = {'Qt'};
else
qhullopts = {'Qt', 'Qx'};
end
end
% Save copies before things get messed up.
Anr = A;
bnr = b;
% First, get rid of any rows of A that are all zero.
Anorms = max(abs(A), [], 2);
badrows = (Anorms == 0);
if any(b(badrows) < 0)
error('A has infeasible trivial rows.')
end
A(badrows, :) = [];
b(badrows) = [];
goodrows = [0; find(~badrows)]; % Add zero for all zero row that gets added.
% Need to find a point in the interior of the polyhedron.
if isempty(x0)
if all(b > 0)
% If b is strictly positive, we know the origin works.
x0 = zeros(size(A, 2), 1);
else
error('Must supply an interior point!');
end
else
x0 = x0(:);
if isrow(x0)
x0 = x0';
end
if length(x0) ~= size(A,2)
error('x0 must have as many entries as A has columns.')
end
if any(A*x0 >= b - tol)
error('x0 is not in the strict interior of Ax <= b!')
end
end
% Now, project the rows of P and find the convex hull.
btilde = b - A*x0;
if any(btilde <= 0)
warning('Shifted b is not strictly positive. convhull will likely fail.')
end
Atilde = [zeros(1, size(A, 2)); bsxfun(@rdivide, A, btilde)];
h = convhulln(Atilde, qhullopts);
u = unique(h(:));
nr = goodrows(u);
if nr(1) == 0
nr(1) = [];
end
h = goodrows(h);
% Finally, grab the appropriate rows for Anr and bnr.
Anr = Anr(nr, :);
bnr = bnr(nr);
end%function
|
computeX1.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62 | function X1 = computeX1(Z, A, B, Xf)
% X1 = computeX1(Z, [A], [B], [Xf])
%
% Computes the feasible set X_1 for the system x^+ = Ax + Bu subject to
% constraints Gx + Hu <= psi and x^+ \in Xf.
%
% Z must be a struct with fields G, H, and psi.
%
% A and B are only necessary if the terminal constraint is given.
%
% Xf can be either a struct with fields A and b to define a polytope, or a
% single vector to define a point constraint. If not provided, it is assumed
% that Xf is the entire space.
%
% X1 is returned as a struct with fields A and b defining a set of inequality
% constraints.
% Check arguments.
narginchk(1, 4);
if ~isstruct(Z) || ~all(isfield(Z, {'G', 'H', 'psi'}))
error('Invalid input for Z!');
end
Nx = size(Z.G, 2);
Nu = size(Z.H, 2);
if nargin() >= 3
sys = struct('A', A, 'B', B); % Save these.
end
% Preallocate constraint matrices.
A = [Z.G, Z.H];
b = Z.psi;
Aeq = zeros(0, Nx + Nu);
beq = zeros(0, 1);
% Do some more stuff if there is a terminal constraint.
if nargin() >= 4 && ~isempty(Xf)
if ~isequal([size(sys.A), size(sys.B)], [Nx, Nx, Nx, Nu])
error('Incorrect size for A or B!');
end
if isstruct(Xf)
% Polyhedron.
if ~all(isfield(Xf, {'A', 'b'}))
error('Struct Xf must have fields A and b!');
end
A = [A; Xf.A*[sys.A, sys.B]];
b = [b; Xf.b];
elseif isvector(Xf) && length(Xf) == Nx
% Terminal equality constraint.
Aeq = [sys.A, sys.B];
beq = Xf;
else
error('Invalid input for Xf!');
end
end
% Now do the projection step.
for i = 1:Nu
[A, b, Aeq, beq] = fouriermotzkin(A, b, Aeq, beq);
end
X1 = struct('A', A, 'b', b);
end%function
|
plotpoly.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | function p = plotpoly(p, varargin)
% p = plotpoly(p, ...)
% p = plotpoly({A, b}, ...)
% p = plotpoly(struct('A', A, 'b', b), ...)
%
% Plots the polyhedron with vertices given in the 2 by N matrix p or given by
% the extreme points of A*x <= b. Any additional arguments are passed to plot.
%
% Returns the extreme points matrix p. If you only want this matrix, pass
% false as the only additional argument, and the plot will not be made.
if nargin() < 1
error('Argument p is required!');
end
% First, find the vertices if {A, b} given.
if iscell(p)
p = halfspace2vertex(p{1}, p{2})';
elseif isstruct(p)
p = halfspace2vertex(p.A, p.b)';
end
% Next, sort the vertices.
ptilde = bsxfun(@rdivide, bsxfun(@plus, p, -mean(p, 2)), std(p, 0, 2));
x = ptilde(1,:);
y = ptilde(2,:);
[th, r] = cart2pol(x, y);
thneg = (th < 0);
th(thneg) = th(thneg) + 2*pi(); % Makes theta in [0, 2*pi] instaed of [-pi, pi].
[~, s] = sortrows([th', r']); % Sort on theta then r.
p = p(:,s);
% Duplicate first data point to give closed cycle.
p = p(:,[1:end,1]);
% Now plot.
if length(varargin) == 0 || ~isequal(varargin{1}, false())
plot(p(1,:), p(2,:), varargin{:});
end
end%function
|
halfspace2vertex.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88 | function [V, nr] = halfspace2vertex(A, b, x0)
% [V, nr] = halfspace2vertex(A, b, [x0])
%
% Finds extreme points of polyhedron A*x <= b. Note that the polyhedron must
% have a point strictly on its interior.
%
% If provided, x0 must be a point on the interior of the polyhedron. If it is
% not given, one is found by solving a linear program.
%
% V is returned as an N by 2 matrix with each row giving an extreme point.
%
% Second output nr is a list of the non-redundant constraints of the polytope.
% Check inputs.
narginchk(2, 3);
Nc = size(A, 1);
Nx = size(A, 2);
if ~isvector(b) || length(b) ~= Nc
error('b is the incorrect size!');
end
b = b(:); % Make sure b is a column vector.
% Sort out interior point.
if nargin() < 3
if all(b > 0)
% The origin is on the interior. Can rescale rows so that b = 1.
x0 = zeros(Nx, 1);
A = bsxfun(@rdivide, A, b);
b = ones(size(b));
else
x0 = findinteriorpoint(A, b);
end
elseif ~isvector(x0) || length(x0) ~= Nx
error('Invalid size for x0!');
end
x0 = x0(:); % Make sure x0 is a column vector.
% Get non-redundant constraints from A and b.
[nr, ~, ~, k] = removeredundantcon(A, b, x0);
% Now loop through facets to find vertices.
V = zeros(size(k, 1), Nx);
keep = true(size(k, 1), 1);
for ix = 1:size(k, 1)
F = A(k(ix,:),:);
g = b(k(ix,:));
[keep(ix), V(ix,:)] = fullranksolve(F, g);
end
V = V(keep,:);
[~, u] = unique(round(V*1e6), 'rows');
V = V(u,:);
% If in 2D, sort the vertices.
if Nx == 2
V = polarsort(V);
end
end%function
function [fullrank, x] = fullranksolve(A, b);
% Checks whether the system is full rank and if so, solves it. If it is not
% full rank, a vector of NaNs are returned.
Nx = size(A, 1);
[U, S, V] = svd(A);
s = diag(S);
tol = Nx*eps(s(1)); % Rank tolerance.
fullrank = all(s >= tol);
if fullrank
x = V*diag(1./s)*U'*b;
else
x = NaN(Nx, 1);
end
end%function
function [p, s] = polarsort(p)
% [p, s] = polarsort(p)
%
% Sorts the [n by 2] matrix p so that the points are counter-clockwise starting
% at the theta = 0 axis. For ties in theta, sorts on radius.
x = p(:,1);
y = p(:,2);
x = (x - mean(x))/std(x); % Normalize so that the origin is at the center.
y = (y - mean(y))/std(y);
[th, r] = cart2pol(x, y);
[~, s] = sortrows([th, r]); % Sort on theta then r.
p = p(s,:);
end%function
|
findinteriorpoint.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92 | function [x0, okay, feas, margin] = findinteriorpoint(A, b, Aeq, beq, tol, maxinside)
% [x0, okay, feas, margin] = findinteriorpoint(A, b, [Aeq], [beq], [tol])
%
% Find a strictly feasible point x0 so that A*x0 <= b - tol. If no such point
% can be found, okay is set to False.
%
% If there is at least a feasible point (but not necessarily on the interior),
% then feas is true, and x0 gives that point. If both okay and feas are false,
% then x0 is meaningless.
%
% margin gives the value e such that A*x0 <= b - e.
%
% The origin is always checked first. If it does not work, an LP is solved
% to find a valid point.
%
% tol is used to decide how much on the interior we need to be. If not
% supplied, the default value is 1e-8*max(1, norm(b)/N). Note that this may
% be too large if b is poorly scaled.
if nargin() < 2
error('A and b are mandatory.')
elseif nargin() < 5
tol = 1e-8*max(1, norm(b)/length(b));
end
if nargin() < 6
maxinside = 1;
else
maxinside = max(tol, maxinside);
end
[m, n] = size(A);
if nargin() < 4 || isempty(Aeq)
Aeq = zeros(0, n);
beq = [];
end
meq = size(Aeq, 1);
okay = false();
% Check whether the origin is on the inside.
if all(abs(beq) < tol) && all(b > tol)
x0 = zeros(n, 1);
okay = true();
feas = true();
margin = min(b);
end
% Try to use fminsearch if there are no equality constraints. Doesn't work
% well if the number of dimensions is very high, so we cap it at 10.
if ~okay && meq == 0 && m <= 10
options = optimset('display', 'off');
[x0, maxr] = fminsearch(@(x) max(max(A*x - b), -1e5*tol), A\b, options);
okay = (maxr < -tol);
feas = okay;
margin = -maxr;
end
% Solve LP otherwise.
if ~okay
c = [zeros(n, 1); -1];
AA = [A, ones(m, 1)];
AAeq = [Aeq, zeros(meq,1)];
lb = [-inf(n, 1); 0];
ub = [inf(n, 1); maxinside];
if isOctave()
ctype = [repmat('U', m, 1); repmat('S', meq, 1)];
[xtilde, ~, err, extra] = glpk(c, [AA; AAeq], [b; beq], lb, ub, ...
ctype, repmat('C', n + 1, 1), 1, struct('msglev', 0));
okay = (err == 0 && extra.status == 5);
else
options = optimoptions('linprog', 'display', 'off', 'algorithm', 'dual-simplex');
[xtilde, ~, exitflag] = linprog(c, AA, b, AAeq, beq, lb, ub, [], options);
okay = (exitflag == 1);
end
if isempty(xtilde)
margin = -inf();
else
margin = xtilde(end); % Amount constraints could be tightened.
end
okay = okay && (margin >= tol);
if isempty(xtilde)
x0 = zeros(n, 1);
okay = false();
else
x0 = xtilde(1:end-1);
end
% Check feasibility of x0.
feas = all(A*x0 - b < tol);
if feas && ~isempty(Aeq)
feas = all(abs(Aeq*x0 - beq) < tol);
end
okay = okay && feas;
end
end%function
|
fouriermotzkin.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104 | function [A, b, Aeq, beq] = fouriermotzkin(A, b, Aeq, beq, ielim)
% [A, b, Aeq, beq] = fouriermotzkin(A, b, [Aeq], [beq], [ielim])
%
% Perform one step of Fourier-Motzkin elimination for the set defined by
%
% {x \in R^n : A*x <= b, Aeq*x = beq}
%
% Note that the inequality constrants can be degenerate, although degeneracy
% will create significantly more constraints compared to explicit equality
% constraints.
%
% Optional argument ielim decides which column to eliminate. Default is the last
% column.
% Check arguments and get sizes.
narginchk(2, 5);
Nlt = size(A, 1);
if ~isvector(b) || length(b) ~= Nlt
error('Invalid size for b!');
end
Nx = size(A, 2);
if nargin() < 3 || isempty(Aeq)
Aeq = zeros(0, Nx);
beq = zeros(0, 1);
Neq = 0;
elseif nargin() < 4
error('beq is required if Aeq is given!');
else
if size(Aeq, 2) ~= Nx
error('Aeq has the wrong number of columns!');
end
Neq = size(Aeq, 1);
if ~isvector(beq) || length(beq) ~= Neq
error('Invalid size for beq!');
end
end
if nargin() < 5
ielim = Nx;
elseif ~isscalar(ielim) || ielim <= 0 || ielim > Nx || round(ielim) ~= ielim
error('ielim must be a scalar positive integer less than Nx!');
end
% Now decide what to do. First, look for an equality constraint with the
% variable of interest.
[pivval, pivrow] = max(abs(Aeq(:,ielim)));
if isempty(pivrow) || pivval == 0
% No suitable equality constraint found. Need to change inequality
% constraints.
[A, b] = fmelim(A, b, ielim);
Aeq(:,ielim) = [];
else
% An equality constraint is available. Handle that.
a = Aeq(pivrow,:);
c = a(ielim);
% Make the pivots.
Aeq = Aeq - Aeq(:,ielim)*a/c;
beq = beq - Aeq(:,ielim)*beq(pivrow)/c;
A = A - A(:,ielim)*a/c;
b = b - A(:,ielim)*beq(pivrow)/c;
% Get rid of the appropriate rows and columns.
A(:,ielim) = [];
Aeq(:,ielim) = [];
Aeq(pivrow,:) = [];
beq(pivrow) = [];
end
% Zap any rows that are all zeros.
[A, b] = removezerorows(A, b);
[Aeq, beq] = removezerorows(Aeq, beq);
end%function
% *****************************************************************************
% Helper Functions
% *****************************************************************************
function [Ae, be] = fmelim(A, b, ielim)
% Performs one step of Fourier-Motzkin elimination for inequality
% constraints.
c = A(:,ielim);
I0 = find(c == 0);
Ip = find(c > 0);
Im = find(c < 0);
Nx = size(A, 2);
Ne = length(I0) + length(Ip)*length(Im);
E = [A(:,1:ielim - 1), A(:,ielim + 1:end), b];
Ee = [E(I0,:); kron(c(Ip), E(Im,:)) - kron(E(Ip,:), c(Im))];
Ae = Ee(:,1:end-1);
be = Ee(:,end);
end%function
function [A, b] = removezerorows(A, b)
% Removes rows of A that are all zeros.
keeprows = any(A, 2);
A = A(keeprows,:);
b = b(keeprows);
end%function
|
vertices2lines.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | function l = vertices2lines(p, xlims, ylims)
% l = vertices2lines(p, xlims, ylims)
%
% Returns 2-column array of line segments corresponding to edges of the
% polygon with vertices in columns of p (which must be in the proper order).
% Each line segment has 101 interpolation points (to make gnuplot happy),
% and there is a row of NaNs inserted between each line.
dp = diff(p, 1, 2);
N = size(p, 2) - 1;
blocks = cell(N, 1);
xlims = linspace(xlims(1), xlims(2), 101)';
ylims = linspace(ylims(1), ylims(2), 101)';
for i = 1:N
slope = dp(2,i)/dp(1,i);
if isinf(slope) || isnan(slope)
x = p(1,i)*[1; 1];
y = ylims;
else
x = xlims;
y = slope*(xlims - p(1,i)) + p(2,i);
end
blocks{i} = [[x, y]; NaN(1, 2)];
end
l = vertcat(blocks{:});
|
