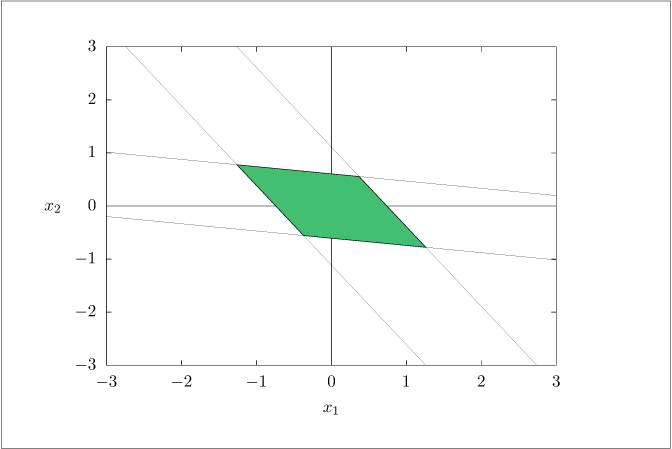
Figure 2.11

% Set computations for Ex. 2.6, 2.7, and 2.8.

% Define model, cost function, and bounds.
A = [2, 1; 0, 2];
B = [1, 0; 0, 1];
N = 3;

alpha = 1e-5;
Q = alpha*eye(2);
R = eye(2);

% Bounds.
xlb = [-5; -inf()];
xub = [5; inf()];
ulb = [-1; -1];
uub = [1; 1];

% Find LQR.

[K, P] = dlqr(A, B, Q, R);
K = -K; % Sign convention.

% Define helper functions.

% Run the computation for a few different cases.
terminals = {'termeq', 'lqr'};
Xn = struct();
V = struct();
Z = struct();
for i = 1:length(terminals)
    t = terminals{i};
    [Xn.(t), V.(t), Z.(t)] = findXn(A, B, K, N, xlb, xub, ulb, uub, t);
    title(t);
end

% Simulate MPC from the initial starting point.
model = struct('A', A, 'B', B, 'N', N);
constraint = Z.lqr;
penalty = struct('Q', Q, 'R', R, 'P', P);
terminal = Xn.lqr{1}; % LQR terminal set.

Nsim = 25;
xsim = zeros(2, Nsim + 1);
xsim(:,1) = [0.5; 0.5]; % Initial condition.
usim = zeros(2, Nsim);
mpcmats = []; % Calculated first time and then reused.
for t = 1:Nsim
    model.x0 = xsim(:,t);
    [xk, uk, ~, status, mpcmats] = linearmpc(model, constraint, penalty, ...
                                             terminal, mpcmats);
    usim(:,t) = uk(:,1);
    xsim(:,t + 1) = xk(:,2);
end

% Now check and see where the finite-horizon control law is the same as the
% infinite-horizon control law.
[x1, x2] = meshgrid(linspace(-1.86, 1.86, 50), linspace(-0.97, 0.97, 50));
x0 = [x1(:), x2(:)]';
terminal = Xn.lqr{1};
X3 = Xn.lqr{end}; % Feasible set.
okaypts = all(bsxfun(@le, X3.A*x0, X3.b));
x0 = x0(:,okaypts); % Get rid of guys that are not feasible to save time.

Npts = size(x0, 2);
ininterior = all(bsxfun(@le, terminal.A*x0, terminal.b)); % See if start in Xf.
mpcmats = [];
for i = 1:Npts
    if ~ininterior(i)
        % Need to check with MPC problem.
        model.x0 = x0(:,i);
        [xk, uk, ~, status, mpcmats] = linearmpc(model, constraint, penalty, ...
                                                 terminal, mpcmats);
        if status.optimal
            % Check whether the ending state is in the interior (with tolerance).
            ininterior(i) = all(terminal.A*xk(:,end) < terminal.b - 1e-3);
        end
    end
end
x0interior = x0(:,ininterior);

% Finally, save data files.
lims = [-10; 10];

pa = V.lqr{1}'; % X_f for LQR (vertices)
palines = vertices2lines(pa', lims, lims); % X_f for LQR (facets)

pb = V.lqr{end}'; % X_n for LQR (vertices)
pblines = vertices2lines(pb', lims, lims); % 'X_n for LQR (facets)

pc = V.termeq{end}'; % X_n for terminal constraint (vertices)

xtable = [0:Nsim; xsim]'; % x timeseries using X_f for LQR

utable = [0:(Nsim - 1); usim]'; % u timeseries using X_f for LQR

pe = x0interior'; % x coordinates where finite-horizon = inf-horizon

save('Xinf.dat', 'pa', 'palines', 'pb', 'pblines', 'pc', ...
     'xtable', 'utable', 'pe');

function [Xn, V, Z] = findXn(A, B, K, N, xlb, xub, ulb, uub, terminal, doplot)
% [Xn, V, Z] = findXn(A, B, K, N, xlb, xub, ulb, uub, terminal, [doplot])
%
% Calculates the various sets for the given system and parameters.
%
% Most inputs are self-explanatory. terminal should be either the string
% 'termeq' to use a terminal equality constraint, or 'lqr' to use the
% maximum LQR-invariant set.
%
% Output Xn is a cell array defining each of the \bbX_n sets. Xn{1} is the
% terminal set, Xn{2} is \bbX_1, etc. V is a cell array with each entry giving
% the extreme vertices of the corresponding Xn (as a 2 by N matrix). Z is a
% structure defining the feasible space.
%
% Also makes a plot of all the sets unless doplot is False.
narginchk(9, 10);
if nargin() < 10
    doplot = true();
end

% Define constraints for Z.
Nx = size(A, 1);
[Az, bz] = hyperrectangle([xlb; ulb], [xub; uub]);
Z = struct('G', Az(:,1:Nx), 'H', Az(:,(Nx + 1):end), 'psi', bz);

% Decide terminal constraint.
switch terminal
case 'termeq'
    % Equality constraint at the origin.
    Xf = [0; 0];
case 'lqr'
    % Build feasible region considering x \in X and Kx \in U.
    [A_U, b_U] = hyperrectangle(ulb, uub);
    A_lqr = A_U*K;
    b_lqr = b_U;
    [A_X, b_X] = hyperrectangle(xlb, xub);
    Acon = [A_lqr; A_X];
    bcon = [b_lqr; b_X];

    % Use LQR-invariant set.
    Xf = struct();
    ApBK = A + B*K; % LQR evolution matrix.
    [Xf.A, Xf.b] = calcOinf(ApBK, Acon, bcon);
    [~, Xf.A, Xf.b] = removeredundantcon(Xf.A, Xf.b);
otherwise
    error('Unknown value for terminal: %s', terminal);
end

% Now do feasible sets computation.
if doplot
    figure();
    hold('on');
    colors = jet(N + 1);
end
Xn = cell(N + 1, 1);
Xn{1} = Xf;
names = cell(N + 1, 1);
names{1} = 'Xf';
V = cell(N + 1, 1);
for n = 1:(N + 1)
    % Plot current set.
    if n > 1
        names{n} = sprintf('X%d', n - 1);
    end
    if doplot
        plotargs = {'-o', 'color', colors(n,:)};
    else
        plotargs = {false()};
    end
    V{n} = plotpoly(Xn{n}, plotargs{:});
    if n == (N + 1)
        break
    end

    % Compute next set. Also need to prune constraints.
    nextXn = computeX1(Z, A, B, Xn{n});
    [~, nextXn.A, nextXn.b] = removeredundantcon(nextXn.A, nextXn.b);
    Xn{n + 1} = nextXn;
end
if doplot
    legend(names{:});
end

end%function

function [Xk, Uk, phi, status, matrices] = linearmpc(model, constraint, penalty, terminal, matrices)
% [Xk, Uk, phi, status, matrices] = linearmpc(model, constraint, penalty, terminal, [matrices])
%
% Solves the following optimization problem:
%
%      N-1
% min  sum [ 1/2(x_k' Q x_k + u_k' R u_k ) ] + 1/2(x_N' P x_n)
% u_k  k=1
%
%    s.t    x_k+1 = A x_k + B u_k
%           G x_k + H u_k <= psi
%           A_f x_N <= b_f
%
% Linear time-invariant MPC.
%
% Input 'model' has the following fields:
% - A: A matrix for system.
% - B: B matrix for system.
% - N: horizon length in number of stemps.
% - x0: initial state of system.
%
% Input 'constraint' has the following fields:
% - G: G matrix for constraints.
% - H: G matrix for constraints.
% - psi: psi vector for constraints.
% Either all or none must be specified.
%
% Input 'penalty' has the following fields:
% - Q: Penalty matricies for state.
% - R: Penalty matrix for input.
% - P: Terminal penalty matrix.
%
% Input terminal can be a vector of length x to specify a terminal equality
% constraint, or a struct with fields A and b (corresponding to A_f and b_f in
% the optimization given above).
%
% The final output matrices is a struct with fields H, f, Alt, blt, Aeq, beq,
% lb, and ub that define the QP formulation. If these are supplied in a struct
% as a fifth argument, only the initial condition model.x0 is updated, and the
% matrices are passed directly to the QP solver. This can save a lot of time if
% you're solving the same problem over and over but with different initial
% conditions. Note that minimal error checking is done

% Check arguments.
narginchk(4, 5);

% Build matrices if not supplied.
if nargin() < 5 || isempty(matrices)
    matrices = buildmatrices(model, constraint, penalty, terminal);
end

% Get sizes.
[numx, numu] = size(model.B);
N = model.N;
numVar = N*(numx + numu) + numx;

% Update initial condition.
matrices.lb(1:numx) = model.x0;
matrices.ub(1:numx) = model.x0; % Fix x0.

% Get vectors to extract x and u from big column vector.
allinds = mod(0:numVar - 1,numx + numu);
xinds = allinds < numx;
uinds = allinds >= numx;

% Solve QP using Octave/Matlab default solver.
if isOctave()
    % Helps to generate a feasible guess.
    uguess = zeros(numu,N);
    xguess = zeros(numx,N+1);
    x0 = model.x0;
    if ~isempty(x0)
        A = model.A;
        B = model.B;
        xguess(:,1) = x0;
        for i = 1:N
            xguess(:,i+1) = A*xguess(:,i) + B*uguess(:,i);
        end
    end
    guess = sparse(numVar, 1);
    guess(xinds) = xguess(:);
    guess(uinds) = uguess(:);
    [X, FVAL, INFO] = qp(guess, matrices.H, matrices.f, ...
        matrices.Aeq, matrices.beq, matrices.lb, matrices.ub, [], ...
        matrices.Alt, matrices.blt);
    status = struct('solver', 'qp', 'flag', INFO.info);
    status.optimal = (status.flag == 0);
else
    % Options for Matlab solver.
    qpoptions = optimoptions('quadprog','display','off');

    % Need to disable a warning.
    STUPIDWARNING = 'optim:quadprog:NullHessian';
    stupidwarningstate = warning('query', STUPIDWARNING);
    warning('off',STUPIDWARNING)

    % Matlab is very fussy about the hessian being exactly symmetric.
    H = matrices.H;
    H = 0.5*(H + H');

    % call solver.
    [X, FVAL, solverflag] = ...
        quadprog(H, matrices.f, matrices.Alt, matrices.blt, ...
        matrices.Aeq, matrices.beq, matrices.lb, matrices.ub, [], qpoptions);
    status = struct('solver', 'quadprog', 'flag', solverflag);
    status.optimal = (status.flag == 1);
    if ~status.optimal
        X = NaN(numVar, 1);
    end

    % reset the state of the warning.
    warning(stupidwarningstate.state, STUPIDWARNING);
end

% Extract x and u from quadprog X.
Xk = reshape(X(xinds), numx, N + 1);
Uk = reshape(X(uinds), numu, N);

phi = FVAL;

end%function

% ******************************************************************************
% Helper function for building matrices.
% ******************************************************************************

function matrices = buildmatrices(model, constraint, penalty, terminal)
% matrices = buildmatrices(model, constraint, penalty, terminal)
%
% Returns the matrices struct used by the main function.

N = model.N;
A = model.A;

if diff(size(A)) ~= 0
    error('model.Ak must be a square matrix.');
end
numx = size(A,1); % Number of states.

B = model.B;
numu = size(B,2); % Number of inputs.

if isfield(constraint,'G')
    G = constraint.G;
    H = constraint.H;
    psi = constraint.psi;
else
    G = zeros(0, numx);

    H = zeros(0, numu);
    psi = zeros(0, 1);
end

% Penalty matrices.
Q = penalty.Q;
R = penalty.R;
P = penalty.P;
M = zeros(numx, numu);

littleH = sparse([Q, M; M', R]);
bigH = kron(eye(N),littleH);
bigH = blkdiag(bigH, P); % Add final penalty matrix.

bigf = zeros(size(bigH, 1), 1);

% Structure of big A (both Aeq and Alt) is
% +-                  -+
% |  A1 A2  0  0  ...  |
% |   0 A1 A2  0  ...  |
% |   0  0 A1 A2  ...  |
% |  ...         A2  0 |
% |  ...         A1 A2 |
% +-                  -+
%
% We construct it first as
%
% +-             -+
% |  ... A1 A2  0 |
% |  ...  0 A1 A2 |
% |  ...  0  0 A1 | <= Note exta A1 that has to be removed.
% +-             -+
%
% and then get rid of extra rows (for last A1) and columns (for
% nonexistant variable u_N).

% For Equalities:
% A1 = [A, B], A2 = [-I, 0].
littleAeq1 = sparse([A, B]);
littleAeq2 = sparse([-eye(size(A)), zeros(size(B))]);

bigAeq = kron(eye(N+1),littleAeq1) + kron(diag(ones(1,N),1),littleAeq2);

bigAeq = bigAeq(1:end-numx,1:end-numu);
    % Remove columns for u_N and for rows of x_N+1 = A x_N + B u_N

bigbeq = zeros(numx*N,1);

% For Inequalities:
% A1 = [G, H], A2 = [0, 0].
littleAlt1 = sparse([G, H]);
littleAlt2 = sparse([zeros(size(G)), zeros(size(G))]);

bigAlt = kron(eye(N+1),littleAlt1) + kron(diag(ones(1,N),1), ...
    littleAlt2);
bigAlt = bigAlt(1:end-size(littleAlt1,1),1:end-numu);
    % Remove columns for u_N and for rows of G x_N + D u_N <= d.
bigblt = repmat(psi, N, 1);

% Variable bounds.
numVar = length(bigf);
LB = -inf*ones(numVar,1);
UB = inf*ones(numVar,1);

% Decide terminal constraint.
if isstruct(terminal) && all(isfield(terminal, {'A', 'b'}))
    Af = terminal.A;
    bf = terminal.b;
    bigAlt = [bigAlt; [sparse(size(Af, 1), numVar - numx), sparse(Af)]];
    bigblt = [bigblt; bf];
elseif isvector(terminal) && length(terminal) == numx
    LB(end-numx+1:end) = terminal;
    UB(end-numx+1:end) = terminal;
elseif isempty(terminal)
    % No terminal constraint. Pass
else
    error('Unknown input for terminal!');
end

% Build struct with appropriate names.
matrices = struct('H', bigH, 'f', bigf, 'Aeq', bigAeq, 'beq', bigbeq, ...
                  'Alt', bigAlt, 'blt', bigblt, 'lb', LB, 'ub', UB);

end%function

function [A, b] = hyperrectangle(lb, ub)
% [A, b] = hyperrectangle(lb, ub)
%
% Returns halfspace representation of hyperrectangle with bounds lb and ub.
% Any infinite or NaN bounds are ignored.

narginchk(2, 2);
if ~isvector(lb) || ~isvector(ub) || length(lb) ~= length(ub)
    error('Inputs must be vectors of the same size!');
end

A = kron(eye(length(lb)), [1; -1]);
b = reshape([ub(:)'; -lb(:)'], 2*length(lb), 1);

goodrows = ~isinf(b) & ~isnan(b);
A = A(goodrows,:);
b = b(goodrows);

end%function

function [AOinf, bOinf, tstar] = calcOinf(F, A, b, tmax)
% [AOinf, bOinf, tstar] = calcOinf(F, A, b, [tmax])
%
% Calculates the maximum admissible set for x^+ = F*x subject to A*x <= b. Note
% that if F is unstable, this procedure will not work.
%
% tmax is the value of t to stop at, as an upper bound is not known a-priori.
% The default value is 100. If this bound is reached without termination, then
% tstar is set to inf.

% Arguments and sizes.
narginchk(3, 4);
if nargin() < 4
    tmax = 100;
end
Nx = size(F, 1);
if size(F, 2) ~= Nx
    error('F must be square!');
end
Nc = size(A, 1);
if size(A, 2) ~= Nx
    error('A must have the same number of columns as F!');
elseif ~isvector(b) || length(b) ~= Nc
    error('b must be a vector with an entry for each row of A!');
end
b = b(:);

% Define linear programming function.

if isOctave()
    solvelp = @solvelp_octave;
else
    solvelp = @solvelp_matlab;
end

% Start the algorithm.
Ft = eye(Nx);
AOinf = zeros(0, Nx);
bOinf = zeros(0, 1);
tstar = inf();

for t = 0:tmax
    % Add constraints for new time point.
    AOinf = [AOinf; A*Ft];
    bOinf = [bOinf; b];

    % Recalculate objective.
    Ft = F*Ft;
    fobj = A*Ft;

    % Maximize each component, stopping early if any bounds are violated.
    okay = true();
    for i = 1:Nc
        [obj, feas] = solvelp(fobj(i,:), AOinf, bOinf);
        if ~feas || obj > b(i)
            okay = false(); % N isn't high enough Need to keep going.
            continue
        end
    end

    % If everything was feasible, then we're done.
    if okay
        tstar = t;
        break
    end
end

end%function

function [obj, feas] = solvelp_octave(f, A, b)
    % Octave version to solve LP.
    Nx = size(A, 2);
    lb = -inf(Nx, 1);
    ub = inf(Nx, 1);
    ctype = repmat('U', size(A, 1), 1);
    vtype = repmat('C', Nx, 1);
    sense = -1; % Maximization.
    [~, obj, err, extra] = glpk(f, A, b, lb, ub, ctype, vtype, sense, ...
                                struct('msglev', 0));
    status = extra.status;
    feas = (err == 0) && (status == 5);
end%function


function [obj, feas] = solvelp_matlab(f, A, b)
    % Matlab version to solve LP.
    prob = struct('f', -f, 'Aineq', A, 'bineq', b, 'options', ...
                  optimoptions('linprog', 'Algorithm', 'dual-simplex', ...
                               'display', 'off'), 'solver', 'linprog');
    [~, obj, exitflag] = linprog(prob);
    obj = -obj; % Fix sign of objective value.
    feas = (exitflag == 1);
end%function

function [nr, Anr, bnr, h, x0] = removeredundantcon(A, b, x0, tol, qhullopts)
% [nr, Anr, bnr, h, x0] = removeredundantcon(A, b, [x0], [tol], qhullopts)
%
% Finds the non-redundant constraints for the polyhedron Ax <= b. nr is a
% column vector with the non-redundant rows. If requested, Anr and bnr are the
% non-redundant parts of A and b.
%
% If x0 is supplied, it must be in the strict interior of A. Otherwise an error
% is thrown. Specifying a valid x0 will speed up the function.
%
% tol is used to decide how much on the interior we need to be. If not supplied,
% the default value is 1e-8*max(1, norm(b)/N). Note that this may be too large
% if b is poorly scaled.
%
% qhullopts is a string of options to pass to qhull. Defaults are described in
% the documentation for convhulln (see `help convhulln`).
%
% h is the output of convhulln, which actually describes the facets, and x0
% is a point on the interior of the polyhedron. Note that if the input
% polyhedron is unbounded, h may have zeros in some entries corresponding to the
% row of all zeros that needs to be added for the method to work.
%
% Note that this requires finding convex hull in N + 1 dimensions, where N
% is the number of columns of A. Thus, this will get very slow if A has a lot
% of columns.
narginchk(2, 5);

% Force b to column vector and check sizes.
b = b(:);
if isrow(b)
    b = b';
end
if size(A, 1) ~= length(b)
    error('A and b must have the same number of rows!');
end
if nargin() < 3
    x0 = [];
end
if nargin() < 4 || isempty(tol)
    tol = 1e-8*max(1, norm(b)/length(b));
elseif tol <= 0
    error('tol must be strictly positive!')
end
if nargin() < 5
    if size(A, 2) <= 4
        qhullopts = {'Qt'};
    else
        qhullopts = {'Qt', 'Qx'};
    end
end


% Save copies before things get messed up.
Anr = A;
bnr = b;

% First, get rid of any rows of A that are all zero.
Anorms = max(abs(A), [], 2);
badrows = (Anorms == 0);
if any(b(badrows) < 0)
    error('A has infeasible trivial rows.')
end
A(badrows, :) = [];
b(badrows) = [];
goodrows = [0; find(~badrows)]; % Add zero for all zero row that gets added.

% Need to find a point in the interior of the polyhedron.
if isempty(x0)
    if all(b > 0)
        % If b is strictly positive, we know the origin works.
        x0 = zeros(size(A, 2), 1);
    else
        error('Must supply an interior point!');
    end
else
    x0 = x0(:);
    if isrow(x0)
        x0 = x0';
    end
    if length(x0) ~= size(A,2)
        error('x0 must have as many entries as A has columns.')
    end
    if any(A*x0 >= b - tol)
        error('x0 is not in the strict interior of Ax <= b!')
    end
end

% Now, project the rows of P and find the convex hull.
btilde = b - A*x0;
if any(btilde <= 0)
    warning('Shifted b is not strictly positive. convhull will likely fail.')
end
Atilde = [zeros(1, size(A, 2)); bsxfun(@rdivide, A, btilde)];
h = convhulln(Atilde, qhullopts);
u = unique(h(:));

nr = goodrows(u);
if nr(1) == 0
    nr(1) = [];
end
h = goodrows(h);

% Finally, grab the appropriate rows for Anr and bnr.
Anr = Anr(nr, :);
bnr = bnr(nr);

end%function

function X1 = computeX1(Z, A, B, Xf)
% X1 = computeX1(Z, [A], [B], [Xf])
%
% Computes the feasible set X_1 for the system x^+ = Ax + Bu subject to
% constraints Gx + Hu <= psi and x^+ \in Xf.
%
% Z must be a struct with fields G, H, and psi.
%
% A and B are only necessary if the terminal constraint is given.
%
% Xf can be either a struct with fields A and b to define a polytope, or a
% single vector to define a point constraint. If not provided, it is assumed
% that Xf is the entire space.
%
% X1 is returned as a struct with fields A and b defining a set of inequality
% constraints.

% Check arguments.
narginchk(1, 4);
if ~isstruct(Z) || ~all(isfield(Z, {'G', 'H', 'psi'}))
    error('Invalid input for Z!');
end
Nx = size(Z.G, 2);
Nu = size(Z.H, 2);
if nargin() >= 3
    sys = struct('A', A, 'B', B); % Save these.
end

% Preallocate constraint matrices.
A = [Z.G, Z.H];
b = Z.psi;
Aeq = zeros(0, Nx + Nu);
beq = zeros(0, 1);

% Do some more stuff if there is a terminal constraint.
if nargin() >= 4 && ~isempty(Xf)
    if ~isequal([size(sys.A), size(sys.B)], [Nx, Nx, Nx, Nu])
        error('Incorrect size for A or B!');
    end
    if isstruct(Xf)
        % Polyhedron.
        if ~all(isfield(Xf, {'A', 'b'}))
            error('Struct Xf must have fields A and b!');
        end
        A = [A; Xf.A*[sys.A, sys.B]];
        b = [b; Xf.b];
    elseif isvector(Xf) && length(Xf) == Nx
        % Terminal equality constraint.
        Aeq = [sys.A, sys.B];
        beq = Xf;
    else
        error('Invalid input for Xf!');
    end
end

% Now do the projection step.
for i = 1:Nu
    [A, b, Aeq, beq] = fouriermotzkin(A, b, Aeq, beq);
end
X1 = struct('A', A, 'b', b);

end%function

function p = plotpoly(p, varargin)
% p = plotpoly(p, ...)
% p = plotpoly({A, b}, ...)
% p = plotpoly(struct('A', A, 'b', b), ...)
%
% Plots the polyhedron with vertices given in the 2 by N matrix p or given by
% the extreme points of A*x <= b. Any additional arguments are passed to plot.
%
% Returns the extreme points matrix p. If you only want this matrix, pass
% false as the only additional argument, and the plot will not be made.
if nargin() < 1
    error('Argument p is required!');
end

% First, find the vertices if {A, b} given.
if iscell(p)
    p = halfspace2vertex(p{1}, p{2})';
elseif isstruct(p)
    p = halfspace2vertex(p.A, p.b)';
end

% Next, sort the vertices.
ptilde = bsxfun(@rdivide, bsxfun(@plus, p, -mean(p, 2)), std(p, 0, 2));
x = ptilde(1,:);
y = ptilde(2,:);
[th, r] = cart2pol(x, y);
thneg = (th < 0);
th(thneg) = th(thneg) + 2*pi(); % Makes theta in [0, 2*pi] instaed of [-pi, pi].
[~, s] = sortrows([th', r']); % Sort on theta then r.
p = p(:,s);

% Duplicate first data point to give closed cycle.
p = p(:,[1:end,1]);

% Now plot.
if length(varargin) == 0 || ~isequal(varargin{1}, false())
    plot(p(1,:), p(2,:), varargin{:});
end
end%function

function [A, b, Aeq, beq] = fouriermotzkin(A, b, Aeq, beq, ielim)
% [A, b, Aeq, beq] = fouriermotzkin(A, b, [Aeq], [beq], [ielim])
%
% Perform one step of Fourier-Motzkin elimination for the set defined by
%
%   {x \in R^n : A*x <= b, Aeq*x = beq}
%
% Note that the inequality constrants can be degenerate, although degeneracy
% will create significantly more constraints compared to explicit equality
% constraints.
%
% Optional argument ielim decides which column to eliminate. Default is the last
% column.

% Check arguments and get sizes.
narginchk(2, 5);
Nlt = size(A, 1);
if ~isvector(b) || length(b) ~= Nlt
    error('Invalid size for b!');
end
Nx = size(A, 2);
if nargin() < 3 || isempty(Aeq)
    Aeq = zeros(0, Nx);
    beq = zeros(0, 1);
    Neq = 0;
elseif nargin() < 4
    error('beq is required if Aeq is given!');
else
    if size(Aeq, 2) ~= Nx
        error('Aeq has the wrong number of columns!');
    end
    Neq = size(Aeq, 1);
    if ~isvector(beq) || length(beq) ~= Neq
        error('Invalid size for beq!');
    end
end
if nargin() < 5
    ielim = Nx;
elseif ~isscalar(ielim) || ielim <= 0 || ielim > Nx || round(ielim) ~= ielim
    error('ielim must be a scalar positive integer less than Nx!');
end

% Now decide what to do. First, look for an equality constraint with the
% variable of interest.
[pivval, pivrow] = max(abs(Aeq(:,ielim)));
if isempty(pivrow) || pivval == 0
    % No suitable equality constraint found. Need to change inequality
    % constraints.
    [A, b] = fmelim(A, b, ielim);
    Aeq(:,ielim) = [];
else
    % An equality constraint is available. Handle that.
    a = Aeq(pivrow,:);
    c = a(ielim);

    % Make the pivots.
    Aeq = Aeq - Aeq(:,ielim)*a/c;
    beq = beq - Aeq(:,ielim)*beq(pivrow)/c;

    A = A - A(:,ielim)*a/c;
    b = b - A(:,ielim)*beq(pivrow)/c;

    % Get rid of the appropriate rows and columns.
    A(:,ielim) = [];
    Aeq(:,ielim) = [];
    Aeq(pivrow,:) = [];
    beq(pivrow) = [];
end

% Zap any rows that are all zeros.
[A, b] = removezerorows(A, b);
[Aeq, beq] = removezerorows(Aeq, beq);

end%function


% *****************************************************************************
% Helper Functions
% *****************************************************************************

function [Ae, be] = fmelim(A, b, ielim)
    % Performs one step of Fourier-Motzkin elimination for inequality
    % constraints.
    c = A(:,ielim);
    I0 = find(c == 0);
    Ip = find(c > 0);
    Im = find(c < 0);

    Nx = size(A, 2);
    Ne = length(I0) + length(Ip)*length(Im);

    E = [A(:,1:ielim - 1), A(:,ielim + 1:end), b];
    Ee = [E(I0,:); kron(c(Ip), E(Im,:)) - kron(E(Ip,:), c(Im))];

    Ae = Ee(:,1:end-1);
    be = Ee(:,end);
end%function

function [A, b] = removezerorows(A, b)
    % Removes rows of A that are all zeros.
    keeprows = any(A, 2);
    A = A(keeprows,:);
    b = b(keeprows);
end%function

function [V, nr] = halfspace2vertex(A, b, x0)
% [V, nr] = halfspace2vertex(A, b, [x0])
%
% Finds extreme points of polyhedron A*x <= b. Note that the polyhedron must
% have a point strictly on its interior.
%
% If provided, x0 must be a point on the interior of the polyhedron. If it is
% not given, one is found by solving a linear program.
%
% V is returned as an N by 2 matrix with each row giving an extreme point.
%
% Second output nr is a list of the non-redundant constraints of the polytope.

% Check inputs.
narginchk(2, 3);
Nc = size(A, 1);
Nx = size(A, 2);
if ~isvector(b) || length(b) ~= Nc
    error('b is the incorrect size!');
end
b = b(:); % Make sure b is a column vector.

% Sort out interior point.
if nargin() < 3
    if all(b > 0)
        % The origin is on the interior. Can rescale rows so that b = 1.
        x0 = zeros(Nx, 1);
        A = bsxfun(@rdivide, A, b);
        b = ones(size(b));
    else
        x0 = findinteriorpoint(A, b);
    end
elseif ~isvector(x0) || length(x0) ~= Nx
    error('Invalid size for x0!');
end
x0 = x0(:); % Make sure x0 is a column vector.

% Get non-redundant constraints from A and b.
[nr, ~, ~, k] = removeredundantcon(A, b, x0);

% Now loop through facets to find vertices.
V = zeros(size(k, 1), Nx);
keep = true(size(k, 1), 1);
for ix = 1:size(k, 1)
    F = A(k(ix,:),:);
    g = b(k(ix,:));
    [keep(ix), V(ix,:)] = fullranksolve(F, g);
end

V = V(keep,:);
[~, u] = unique(round(V*1e6), 'rows');
V = V(u,:);

% If in 2D, sort the vertices.
if Nx == 2
    V = polarsort(V);
end

end%function

function [fullrank, x] = fullranksolve(A, b);
    % Checks whether the system is full rank and if so, solves it. If it is not
    % full rank, a vector of NaNs are returned.
    Nx = size(A, 1);
    [U, S, V] = svd(A);
    s = diag(S);
    tol = Nx*eps(s(1)); % Rank tolerance.
    fullrank = all(s >= tol);
    if fullrank
        x = V*diag(1./s)*U'*b;
    else
        x = NaN(Nx, 1);
    end
end%function

function [p, s] = polarsort(p)
    % [p, s] = polarsort(p)
    %
    % Sorts the [n by 2] matrix p so that the points are counter-clockwise starting
    % at the theta = 0 axis. For ties in theta, sorts on radius.
    x = p(:,1);
    y = p(:,2);
    x = (x - mean(x))/std(x); % Normalize so that the origin is at the center.
    y = (y - mean(y))/std(y);
    [th, r] = cart2pol(x, y);
    [~, s] = sortrows([th, r]); % Sort on theta then r.
    p = p(s,:);
end%function

function [x0, okay, feas, margin] = findinteriorpoint(A, b, Aeq, beq, tol, maxinside)
% [x0, okay, feas, margin] = findinteriorpoint(A, b, [Aeq], [beq], [tol])
%
% Find a strictly feasible point x0 so that A*x0 <= b - tol. If no such point
% can be found, okay is set to False.
%
% If there is at least a feasible point (but not necessarily on the interior),
% then feas is true, and x0 gives that point. If both okay and feas are false,
% then x0 is meaningless.
%
% margin gives the value e such that A*x0 <= b - e.
%
% The origin is always checked first. If it does not work, an LP is solved
% to find a valid point.
%
% tol is used to decide how much on the interior we need to be. If not
% supplied, the default value is 1e-8*max(1, norm(b)/N). Note that this may
% be too large if b is poorly scaled.
if nargin() < 2
    error('A and b are mandatory.')
elseif nargin() < 5
    tol = 1e-8*max(1, norm(b)/length(b));
end
if nargin() < 6
    maxinside = 1;
else
    maxinside = max(tol, maxinside);
end
[m, n] = size(A);
if nargin() < 4 || isempty(Aeq)
    Aeq = zeros(0, n);
    beq = [];
end
meq = size(Aeq, 1);
okay = false();

% Check whether the origin is on the inside.
if all(abs(beq) < tol) && all(b > tol)
    x0 = zeros(n, 1);
    okay = true();
    feas = true();
    margin = min(b);
end

% Try to use fminsearch if there are no equality constraints. Doesn't work
% well if the number of dimensions is very high, so we cap it at 10.
if ~okay && meq == 0 && m <= 10
    options = optimset('display', 'off');
    [x0, maxr] = fminsearch(@(x) max(max(A*x - b), -1e5*tol), A\b, options);
    okay = (maxr < -tol);
    feas = okay;
    margin = -maxr;
end

% Solve LP otherwise.
if ~okay
    c = [zeros(n, 1); -1];
    AA = [A, ones(m, 1)];
    AAeq = [Aeq, zeros(meq,1)];
    lb = [-inf(n, 1); 0];
    ub = [inf(n, 1); maxinside];
    if isOctave()
        ctype = [repmat('U', m, 1); repmat('S', meq, 1)];
        [xtilde, ~, err, extra] = glpk(c, [AA; AAeq], [b; beq], lb, ub,  ...
            ctype, repmat('C', n + 1, 1), 1, struct('msglev', 0));
        okay = (err == 0 && extra.status == 5);
    else
        options = optimoptions('linprog', 'display', 'off', 'algorithm', 'dual-simplex');
        [xtilde, ~, exitflag] = linprog(c, AA, b, AAeq, beq, lb, ub, [], options);
        okay = (exitflag == 1);
    end
    if isempty(xtilde)
        margin = -inf();
    else
        margin = xtilde(end); % Amount constraints could be tightened.
    end
    okay = okay && (margin >= tol);
    if isempty(xtilde)
        x0 = zeros(n, 1);
        okay = false();
    else
        x0 = xtilde(1:end-1);
    end

    % Check feasibility of x0.
    feas = all(A*x0 - b < tol);
    if feas && ~isempty(Aeq)
        feas = all(abs(Aeq*x0 - beq) < tol);
    end
    okay = okay && feas;
end
end%function

function l = vertices2lines(p, xlims, ylims)
    % l = vertices2lines(p, xlims, ylims)
    %
    % Returns 2-column array of line segments corresponding to edges of the
    % polygon with vertices in columns of p (which must be in the proper order).
    % Each line segment has 101 interpolation points (to make gnuplot happy),
    % and there is a row of NaNs inserted between each line.
    dp = diff(p, 1, 2);
    N = size(p, 2) - 1;
    blocks = cell(N, 1);
    xlims = linspace(xlims(1), xlims(2), 101)';
    ylims = linspace(ylims(1), ylims(2), 101)';
    for i = 1:N
        slope = dp(2,i)/dp(1,i);
        if isinf(slope) || isnan(slope)
            x = p(1,i)*[1; 1];
            y = ylims;
        else
            x = xlims;
            y = slope*(xlims - p(1,i)) + p(2,i);
        end
        blocks{i} = [[x, y]; NaN(1, 2)];
    end
    l = vertcat(blocks{:});

Figure 2.11:

The region \mathbb {X}_f, in which the unconstrained LQR control law is feasible for Exercise \ref {exer:Xinf}.

Code for Figure 2.11

main.m

findXn.m

linearmpc.m

hyperrectangle.m

calcOinf.m

removeredundantcon.m

computeX1.m

plotpoly.m

fouriermotzkin.m

halfspace2vertex.m

findinteriorpoint.m

vertices2lines.m