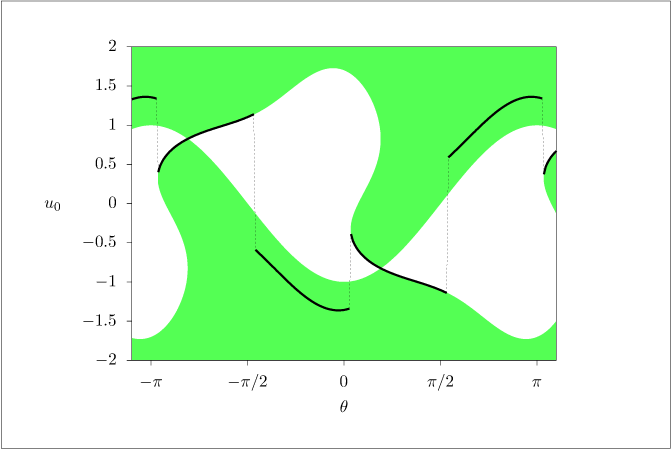
Figure 2.3:

First element of control constraint set \mathcal {U}_3(x) (shaded) and control law \kappa _3(x) (line) versus x=(\cos (\theta ),\sin (\theta )), \theta \in [-\pi ,\pi ] on the unit circle for a nonlinear system with terminal constraint.

Code for Figure 2.3

Text of the GNU GPL.

main.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
% Finding the feasible region and optimal solution of the (u, u^3) example.
thmin = -1.1;
thmax = 1.1;

% Need to sample with higher density for this boundary.
theta = linspace(thmin, thmax, 1001);

% Points on unit circle.
x = cos(pi()*theta);
y = sin(pi()*theta);

% Weird curvy branch for numerator = 0.
numcurves = NaN(3, length(theta));
for i = 1:length(theta)
    r = roots([3, -3*x(i), -3*x(i)^2, -x(i)^3 + 4*y(i)]);
    r(abs(imag(r)) > 1e-6) = NaN();
    numcurves(:,i) = real(r);
end

% Nice branch where denominator = 0.
dencurve = -x;

% Need to do some magic to plot the curve properly because it's a multivalued
% function. Loop through the points, finding the next closest one at each step.
% This works because the curve is not self-intersecting and we know one of the
% endpoints. We bring the nice denominator curve along for the ride so that
% the region is easier to plot later on.
[inum, jnum] = find(~isnan(numcurves));
z = [numcurves(sub2ind(size(numcurves), inum, jnum))'; dencurve(jnum); ...
     theta(jnum)];
zscale = max(z, [], 2) - min(z, [], 2);
z = bsxfun(@rdivide, z, zscale);
for i = 2:size(z, 2)
    dist = [1, 0, 1]*bsxfun(@minus, z(:,i:end), z(:,i - 1)).^2;
    [~, inext] = min(dist);
    inext = inext + i - 1; % Correct for offset.
    if inext ~= i
        z(:,[i, inext]) = z(:,[inext, i]);
    end
end
z = bsxfun(@times, z, zscale); % Rescale.
ufeas1 = max(z(1:2,:)); % Top piece.
ufeas2 = min(z(1:2,:)); % Bottom piece.
thfeas = z(3,:);

% Now find the minimizer. We use a coarser gridding here.
theta = linspace(thmin, thmax, 241);

urange = linspace(-2, 2, 1001);
[th, u] = meshgrid(theta, urange);
Vplus = cost(u, th, 1);
Vminus = cost(u, th, -1);
[V, firstsign] = min(cat(3, Vplus, Vminus), [], 3);
firstsign = 3 - 2*firstsign;

% Find local minima.
Vmid = V(2:end-1,:); % Slice out edges.
localmin = (Vmid < V(1:end-2,:)) & (Vmid < V(3:end,:));
localmin = [false(size(theta)); localmin; false(size(theta))]; % Add edges back.

ilocal = find(localmin(:));
Vlocal = V(ilocal);
thlocal = th(ilocal);
ulocal = u(ilocal);

% Find the absolute minima. Run fminsearch to refine a bit.
[Vmin, imin] = min(V);
umin = urange(imin);
for i = 1:length(umin)
    [umin(i), Vmin(i)] = fminsearch(@(u) cost(u, theta(i), ...
                                              firstsign(imin(i),i)), umin(i));
end

% Find lines of discontinuity.
[upieces, ujumps] = getdiscont(theta, umin, 2);
[Vpieces, Vjumps] = getdiscont(theta, Vmin, 2);

% Make a plot of u.
figure();
hold('on');
ufill = [ufeas1, ufeas2(end:-1:1)];
thfill = [thfeas, thfeas(end:-1:1)];
fill(thfill, ufill, 'r', 'edgecolor', 'r');
plot(thlocal, ulocal, 'sb', upieces(:,1), upieces(:,2), '-g', ...
     ujumps(:,1), ujumps(:,2), ':g');
legend('Infeasible', 'Local Optima', 'Global Optima');
xlabel('\theta/\pi');
ylabel('Input');

% Make a plot of V.
figure();
hold('on');
semilogy(thlocal, Vlocal, 'sr', Vpieces(:,1), Vpieces(:,2), '-g', ...
         Vjumps(:,1), Vjumps(:,2), ':g');
xlabel('\theta/\pi');
ylabel('Cost');

% Now save data.
feas = [thfeas', ufeas1', ufeas2'];
save('circle.dat', 'upieces', 'ujumps', 'Vpieces', 'Vjumps', 'feas');

cost.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function V = cost(u, th, firstsign)
    % Computes optimal cost with inf if infeasible.
    narginchk(3, 3);
    x = cos(pi()*th);
    y = sin(pi()*th);

    % Calculate b.
    bnum = 3*u.^3 - 3*x.*u.^2 - 3*x.^2.*u - x.^3 + 4*y;
    bden = 12*(u + x);
    b = bnum./bden;

    % Simulate the system.
    useq = {u, -x/2 - u/2 + firstsign*sqrt(b), -x/2 - u/2 - firstsign*sqrt(b)};
    V = 0;
    for i = 1:4
        V = V + x.^2 + y.^2;
        if i == 4
            break
        end
        V = V + useq{i}.^2;
        x = x + useq{i};
        y = y + useq{i}.^3;
    end
    V = real(V);
    V(b < 0) = inf(); % These points are infeasible.

getdiscont.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function [pieces, jumps] = getdiscont(x, y, N)
    % Finds discontinuities in y and adds in NaNs to make a gap.
    dy = abs(diff(y));
    idiscont = find(dy > mean(dy) + N*std(dy));

    % Interpolate x and y, screening out any large jumps.
    expand = @(z) [z; z(1:end-1) + 0.5*diff(z), NaN()];
    x = expand(x);
    xdc1 = x(1,idiscont);
    xdc2 = x(1,idiscont + 1);
    x(2,idiscont) = NaN();

    y = expand(y);
    ydc1 = y(1,idiscont);
    ydc2 = y(1,idiscont + 1);
    y(2,idiscont) = NaN();

    % Assemble discontinuities for plotting.
    xdc = [xdc1; xdc2; NaN(size(xdc2))];
    ydc = [ydc1; ydc2; NaN(size(ydc2))];

    % Package everybody up.
    pieces = [x(:), y(:)];
    jumps = [xdc(:), ydc(:)];