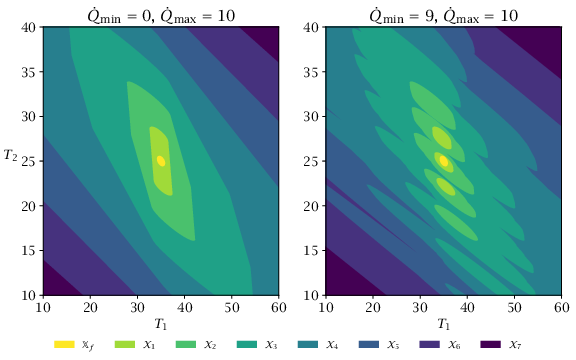
Figure 2.8:

Feasible sets \mathcal {X}_N for two values of \dot {Q}_min. Note that for \dot {Q}_min=9 (right-hand side), \mathcal {X}_N for N \leq 4 are disconnected sets.

Code for Figure 2.8

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
% Calculation of X_n sets for a linear system with discrete actuators.
% Note that for computational purposes, we use a polyhedral approximation of
% the true elliptical X_n.



sys = getcooler();
Qmax = sys.Qmax;
Qmin = sys.Qmin;
ns = sys.ns;
A = sys.A;
B = sys.B(:,1); % Second input doesn't affect dynamics.
F = sys.F;
P = sys.Xf.P;
xss = sys.xss;
rho = sys.Xf.rho;

Xf = ellipseterm(A, P, xss, rho, 32);




% Calculate feasible sets.
Ucontinuous = {[0, max(ns)*Qmax]};
Udiscrete = arrayfun(@(n) n*[Qmin, Qmax], ns, 'UniformOutput', false());

N = 7;
Xc = calcXn(A, B, F, N, Xf, Ucontinuous);
Xd = calcXn(A, B, F, N, Xf, Udiscrete);

% Make a plot.

fprintf('Plotting. May take some time.\n');
figure();
lims = [sys.T1ss + 25*[-1, 1], sys.T2ss + 15*[-1, 1]];

subplot(1, 2, 1);
plotXn(Xc, lims);
title('Q_{min} = 0, Q_{max} = 10');

subplot(1, 2, 2);
plotXn(Xd, lims);
title('Q_{min} = 9, Q_{max} = 10');

getcooler.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
function sys = getcooler()
% sys = getcooler()
%
% Returns a struct of parameters for the cooler system.
narginchk(0, 0);

% Define system.
Nx = 2;
Nu = 2;
alpha = 2;
beta = 1;
rho1 = 1;
rho2 = 1;

ns = [0, 1, 2];
Qmin = 9;
Qmax = 10;

nss = 1;
Qss = nss*Qmax;

uss = [Qss; nss];

T0 = 40;
T1ss = 35;
T2ss = 25;

xss = [T1ss; T2ss];

% Continuous-time system.
a = [-alpha - rho1, rho1; rho2, -rho2];
b = [0, 0; -beta, 0];
f = [alpha*T0; 0];

% Discretize.
Delta = 0.25;
A = expm(Delta*a);
B = a\(A - eye(2))*b;
F = a\(A - eye(2))*f;

% Choose penalty.
Q = eye(Nx);
R = eye(Nu);

% Pick terminal region.
Xf = struct('rho', 1, 'P', dlyap(A, Q)); % Level set for Xf.

% Save everything to a struct.
fields = who();
sys = struct();
for i = 1:length(fields)
    f = fields{i};
    sys.(f) = eval(f);
end

end%function

ellipseterm.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
function Xf = ellipseterm(A, P, xss, rho, n)
    % Xf = ellipseterm(A, P, xss, rho, n)
    %
    % Returns a polyhedral tangent approximation of an ellipsoidal terminal set.
    % Also makes a plot of the evolution of Xf under A.
    %
    % Xf is a 2 by n matrix of extreme points. A and b are the polyhedral
    % representation of Xf. P is the terminal penalty weight.
    narginchk(5, 5);

    [v, l] = eig(P/rho);

    a = 1/sqrt(l(1,1));
    b = 1/sqrt(l(2,2));
    calc = @(t) v(:,1)*a*cos(t) + v(:,2)*b*sin(t);

    T = linspace(0, 2*pi(), n + 1);
    t = linspace(0, 2*pi(), 10*n + 1);

    E = calc(T);
    AE = A*E;

    e = calc(t);
    Ae = A*e;

    figure();
    hold('on');
    plot(E(1,:) + xss(1), E(2,:) + xss(2), '-ob', 'DisplayName', 'X_f');
    plot(e(1,:) + xss(1), e(2,:) + xss(2), '--b');
    plot(AE(1,:) + xss(1), AE(2,:) + xss(2), '-or', ...
         'DisplayName', 'f(X_f, \kappa_f(X_f))');
    plot(Ae(1,:) + xss(1), Ae(2,:) + xss(2), '--r');
    xlabel('T_1');
    ylabel('T_2', 'rotation', 0);
    title(sprintf('Terminal Region X_f = {x | x''Px <= %g}', rho));
    legend('location', 'NorthEast');

    Xf = bsxfun(@plus, xss, E(:,1:(end - 1)));

addpoints.m

1
2
3
4
5
function p = addpoints(p1, p2)
    % Adds two arrays of points (2D with rows x and y).
    p = bsxfun(@plus, p1, permute(p2, [1, 3, 2]));
    psize = size(p);
    p = reshape(p, psize(1), psize(2)*psize(3));

minkowski.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function p = minkowski(p1, p2)
    % Returns minkowski sum of extreme point polytopes p and q. Only works
    % for two dimensions.
    narginchk(1, 2);
    if nargin() < 2
        p2 = [0; 0];
    end
    p = addpoints(p1, p2);
    ch = convhull(p(1,:), p(2,:));
    p = p(:,ch(2:end));

calcXn.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function Xn = calcXn(A, B, f, N, Xf, U, x0)
    % Calculate X_n sets for the system
    %
    %     x^+ = Ax + Bu + f
    %
    % Xf should be an extreme point representation of Xf, and U should be a
    % cell array of extreme-point polytopes for U.
    narginchk(6, 6);
    Ainv = inv(A);
    BU = cellfun(@(u) B*u + f, U, 'UniformOutput', false());
    Xn = cell(N + 1, 1);
    Xn{1} = {Xf};
    fprintf('*** Calculating Xk (max k = %d) ***\n', N);
    for n = 2:(N + 1)
        Xn{n} = cell(length(Xn{n - 1}), length(BU));
        for i = 1:length(Xn{n - 1})
            xn = Xn{n - 1}{i};
            for j = 1:length(BU)
                bu = BU{j};
                Xn{n}{i, j} = Ainv*minkowski(xn, -bu);
            end
        end
        Xn{n} = Xn{n}(:); % Flatten to a single list.
        fprintf('   k = %d: %d regions\n', n - 1, length(Xn{n}));
    end

plotXn.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function plotXn(Xn, lims)
    % Plots a set of regions on the current axes.
    narginchk(1, 2);
    if nargin() >= 2
        axis(lims);
    end
    hold('on');
    if exist('viridis') == 2
        cmap = @viridis;
    elseif exist('parula') == 2
        cmap = @parula;
    else
        cmap = @jet;
    end
    colors = flipud(cmap(length(Xn)));
    for n = length(Xn):-1:1
        xn = Xn{n};
        for i = 1:length(xn)
            patch(xn{i}(1,:), xn{i}(2,:), -n*ones(1, size(xn{i}, 2)), ...
                  colors(n,:), 'EdgeColor', 'none');
        end
    end
    xlabel('T_1');
    ylabel('T_2', 'rotation', 0);