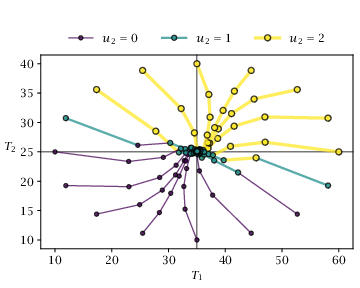
Figure 2.9:

Phase portrait for closed-loop evolution of cooler system with \dot {Q}_min=9. Line colors show value of discrete actuator u_2.

Code for Figure 2.9

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
% Closed-loop optimization of cooler system.



mpc = import_mpctools();

% Get system.
sys = getcooler();
Nx = sys.Nx;
Nu = sys.Nu;
xss = sys.xss;
uss = sys.uss;
f = mpc.getCasadiFunc(@(x, u) sys.A*x + sys.B*u + sys.F, ...
                      [Nx, Nu], {'x', 'u'}, {'f'});

% Choose cost function.
Q = sys.Q;
R = 0.001*sys.R; % Turn down this penalty.
P = sys.Xf.P;
l = mpc.getCasadiFunc(@(x, u, xss, uss) (x - xss)'*Q*(x - xss) ...
                      + (u - uss)'*R*(u - uss), [Nx, Nu, Nx, Nu], ...
                      {'x', 'u', 'xss', 'uss'}, {'l'});
Vf = mpc.getCasadiFunc(@(x, xss) (x - xss)'*P*(x - xss), [Nx, Nx], ...
                       {'x', 'xss'}, {'Vf'});

% Define input constraints and terminal constraint.
Qmin = sys.Qmin;
Qmax = sys.Qmax;
e = mpc.getCasadiFunc(@(u) [u(1) - u(2)*Qmax; u(2)*Qmin - u(1)], ...
                      [Nu], {'u'}, {'e'});

udiscrete = [false(); true()];

rho = sys.Xf.rho; % Level set for terminal region.
ef = mpc.getCasadiFunc(@(x, xss) (x - xss)'*P*(x - xss) - rho, ...
                       [Nx, Nx], {'x', 'xss'}, {'ef'});

% Build controller.
Nt = 8;
N = struct('x', Nx, 'u', Nu, 't', Nt);
par = struct('xss', xss, 'uss', uss);
lb = struct('u', [0; 0]);
nmax = max(sys.ns);
ub = struct('u', [nmax*Qmax; nmax]);
controller = mpc.nmpc('f', f, 'l', l, 'Vf', Vf, 'e', e, 'ef', ef, ...
                      'N', N, 'lb', lb, 'ub', ub, ...
                      'par', par, 'udiscrete', udiscrete, ...
                      'solver', 'bonmin', 'verbosity', 0);

% Run closed-loop simulation for various initial conditions.
Nx0 = 16;
theta = linspace(0, 2*pi(), Nx0 + 1);
theta = theta(2:end);
x0 = bsxfun(@plus, xss, [25*cos(theta); 15*sin(theta)]);
Nsim = 16;
x = NaN(Nx, Nsim + 1, Nx0);
u = NaN(Nu, Nsim, Nx0);
for j = 1:Nx0
    x(:,1,j) = x0(:,j);
    for i = 1:Nsim
        controller.fixvar('x', 1, x(:,i,j));
        controller.solve();
        if ~isequal(controller.status, 'SUCCESS')
            warning('Solver failed at time %d (%s)!', i, controller.status);
            break
        end
        u(:,i,j) = controller.var.u(:,1);
        x(:,i + 1,j) = controller.var.x(:,2);
    end
end

% Make phase plot.
lims = [sys.T1ss + 25*[-1, 1], sys.T2ss + 15*[-1, 1]];
colors = {'r', 'c', 'b'};
labels = {'n = 0', 'n = 1', 'n = 2'};
figure();
hold('on');
axis(lims);
for j = 1:Nx0
    for i = 1:Nsim
        line(x(1,i:(i + 1),j), x(2,i:(i + 1),j), ...
             'color', colors{u(2,i,j) + 1});
    end
end
for k = 1:3
    plot(NaN(), NaN(), ['-', colors{k}], 'DisplayName', labels{k});
end
legend('location', 'NorthEast');

getcooler.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
function sys = getcooler()
% sys = getcooler()
%
% Returns a struct of parameters for the cooler system.
narginchk(0, 0);

% Define system.
Nx = 2;
Nu = 2;
alpha = 2;
beta = 1;
rho1 = 1;
rho2 = 1;

ns = [0, 1, 2];
Qmin = 9;
Qmax = 10;

nss = 1;
Qss = nss*Qmax;

uss = [Qss; nss];

T0 = 40;
T1ss = 35;
T2ss = 25;

xss = [T1ss; T2ss];

% Continuous-time system.
a = [-alpha - rho1, rho1; rho2, -rho2];
b = [0, 0; -beta, 0];
f = [alpha*T0; 0];

% Discretize.
Delta = 0.25;
A = expm(Delta*a);
B = a\(A - eye(2))*b;
F = a\(A - eye(2))*f;

% Choose penalty.
Q = eye(Nx);
R = eye(Nu);

% Pick terminal region.
Xf = struct('rho', 1, 'P', dlyap(A, Q)); % Level set for Xf.

% Save everything to a struct.
fields = who();
sys = struct();
for i = 1:length(fields)
    f = fields{i};
    sys.(f) = eval(f);
end

end%function