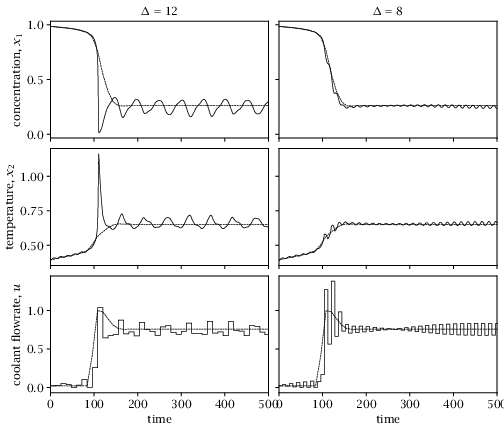
Figure 3.8:

Concentration versus time for the ancillary model predictive controller with sample time \Delta =12 (left) and \Delta =8 (right).

Code for Figure 3.8

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
% Robust control of an exothermic reaction.

% Load parameters for problem.
nompars = cstrparam();
nompars.tfinal = 600;
nompars.colloc = 10;
nompars.plantSteps = 20;

% Disturbance.
nompars.A = 0.002;
nompars.w = 0.4;

% Different sample times.
Deltas = [8, 12];
pars = struct();
for i = 1:length(Deltas)
    f = sprintf('d%d', Deltas(i));
    pars.(f) = nompars;
    pars.(f).Delta = Deltas(i);
end
pars.d12.colloc = 24; % Need more points for longer sample time.
fields = fieldnames(pars);

% Prediction Horizon is same.
predHorizon = 360;
for i = 1:length(fields)
    f = fields{i};
    pars.(f).N = round(predHorizon/pars.(f).Delta);
end

% Run nominal (central path) MPC using sample time of 12. Then resample.
reftraj = nominalmpc(pars.d12);


% Run tube-based MPC multiple times.
results = struct();
for i = 1:length(fields)
    f = fields{i};
    pars.(f).reftraj = resample_nominal(reftraj, pars.(f).Delta);
    results.(f) = tubempc(pars.(f));
end

% Make plot.
figure();
Nrows = 3;
Ncols = length(fields);
ylabels = {'concentration', 'temperature', 'coolant flow'};
ylims = {[0, 1], [0.3, 0.8], [-0.1, 1.4]};
for j = 1:Ncols
    f = fields{j};
    for i = 1:Nrows
        subplot(Nrows, Ncols, (i - 1)*Ncols + j);
        hold('on');
        if i == 3
            stairs(results.(f).t, results.(f).u([1:end,end]), '-k');
            stairs(reftraj.t, reftraj.u([1:end,end]), '--b');
        else
            plot(results.(f).t, results.(f).x(i,:), '-k', ...
                 reftraj.t, reftraj.x(i,:), '--b');
        end
        xlim([0, 500]);
        ylim(ylims{i});
        if i == 1
            title(sprintf('Delta = %s', f(2:end)));
        elseif i == Nrows
            xlabel('Time');
        end
        if j == 1
            ylabel(ylabels{i});
        end
    end
end

nominalmpc.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
function reference_trajectory = nominalmpc(pars)
% reference_trajectory = nominalmpc(pars)
%
% Runs nominal NMPC for CSTR example in Chapter 3 to generate the reference
% trajectory for tube-based MPC.
%
% Note: In this script, "p" denotes the disturbance ("w" in MPC textbook).

mpc = import_mpctools();

% Read parameters.
Nu = pars.Nu;
Np = pars.Np;
Delta = pars.Delta;
tfinal = pars.tfinal;
N = pars.N;
uprev = pars.uprev;
usp = pars.usp;

% Add time state.
Nx = pars.Nx + 1;
xub = [pars.xub; Inf];
xlb = [pars.xlb; -Inf];
x0 = [pars.x0; 0];
ze = [pars.ze; tfinal];

% Tightened constraints for nominal problem.
uub = pars.uub_nominal;
ulb = pars.ulb_nominal;

% Make functions.
ode_model = @(x, u) pars.ode(x, u, 0, pars);
ode_plant = @(x, u, p) pars.ode(x, u, p, pars);
ode_casadi = mpc.getCasadiFunc(ode_model, [Nx, Nu], ...
                               {'x', 'u'}, {'cstr_model'});
cstrsim = mpc.getCasadiIntegrator(ode_plant, Delta, [Nx, Nu, Np], ...
                                  {'x', 'u', 'p'}, {'cstr_plant'});

stagecost_casadi = @(x, u, xsp, usp) stagecost(x, u, xsp, usp, pars);
termcost_casadi = @(x, xsp) termcost(x, xsp, pars);
l = mpc.getCasadiFunc(stagecost_casadi, [Nx, Nu, Nx, Nu], {'x', 'u', 'xsp', 'usp'}, {'l'});
Vf = mpc.getCasadiFunc(termcost_casadi, [Nx, Nx], {'x', 'xsp'}, {'Vf'});

% Make NMPC controller.
Ncontrol = struct('x', Nx, 'u', Nu, 't', N);
values.xsp = repmat(ze, 1, N + 1);
values.usp = repmat(usp, 1, N);
guess.x = [linspace(x0(1), ze(1), N + 1); linspace(x0(2), ze(2), N + 1); ...
    linspace(x0(3), x0(3) + N*Delta, N + 1)];
guess.u = linspace(uprev, usp, N);
Ncontrol.c = pars.colloc;

% Avoid using terminal constraint (use high terminal penalty instead so
% that ipopt can solve the problem).
solverNMPC = mpc.nmpc('f', ode_casadi, 'N', Ncontrol, 'Delta', Delta, ...
                      'verbosity', 0, 'l', l, 'Vf', Vf, ...
                      'x0', x0, 'guess', guess, 'par', values, ...
                      'lb', struct('x', xlb*ones(1, N + 1), 'u', ulb*ones(Nu, N)), ...
                      'ub', struct('x', xub*ones(1, N + 1), 'u', uub*ones(Nu, N)));

% Closed-loop simulation.
Nsim = tfinal/Delta + N;
x = NaN(Nx, Nsim + 1);
x(:, 1) = x0;
u = NaN(Nu, Nsim);

for i = 1:Nsim
    % Set initial condition and solve.
    solverNMPC.fixvar('x', 1, x(:, i));
    solverNMPC.solve();

    % Print status.
    fprintf('%d: %s\n', i, solverNMPC.status);
    if ~isequal(solverNMPC.status, 'Solve_Succeeded')
        warning('Failed at time %d!', i);
        break
    end%if

    % Inject control and simulate plant.
    u(:,i) = solverNMPC.var.u(:,1);
    x(:,i + 1) = full(cstrsim(x(:,i), u(:,i), 0));
    solverNMPC.saveguess();
end%for

% Save data.
t = Delta*(0:Nsim)';
reference_trajectory = struct();
reference_trajectory.x = x;
reference_trajectory.u = u;
reference_trajectory.t = t;

end%function

function l = stagecost(x, u, xsp, usp, pars)
    % Quadratic stage cost.
    Q = pars.Q;
    R = pars.R;
    xerr = x(1:pars.Nx) - xsp(1:pars.Nx);
    uerr = u - usp;
    l = Q*(xerr'*xerr) + R*(uerr'*uerr);
end%function

function Vf = termcost(x, xsp, pars)
    % Quadratic terminal penalty.
    Qf = pars.Qf;
    xerr = x(1:pars.Nx) - xsp(1:pars.Nx);
    Vf = Qf*(xerr'*xerr);
end%function

tubempc.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
function result = tubempc(pars)
% result = tubempc(pars)
%
% Runs tube-based NMPC for CSTR example in Chapter 3.
%
% Note: In this script, "p" denotes the disturbance ("w" in MPC textbook).

mpc = import_mpctools();

% Read parameters.
Nu = pars.Nu;
Np = pars.Np;
Delta = pars.Delta;
uub = pars.uub;
ulb = pars.ulb;
tfinal = pars.tfinal;
N = pars.N;
plantSteps = pars.plantSteps;

% Add time state.
Nx = pars.Nx + 1;
xub = [pars.xub; Inf];
xlb = [pars.xlb; -Inf];
x0 = [pars.x0; 0];

% Get reference trajectories.
xsp = pars.reftraj.x;
usp = pars.reftraj.u;

% Make functions.
ode_model = @(x, u) pars.ode(x, u, 0, pars);
ode_plant = @(x, u, p) pars.ode(x, u, p, pars);
ode_casadi = mpc.getCasadiFunc(ode_model, [Nx, Nu], ...
                               {'x', 'u'}, {'cstr_model'});
cstrsim = mpc.getCasadiIntegrator(ode_plant, Delta/plantSteps, [Nx, Nu, Np], ...
                                  {'x', 'u', 'p'}, {'cstr_plant'});

stagecost_casadi = @(x, u, xsp, usp) stagecost(x, u, xsp, usp, pars);
termcost_casadi = @(x, xsp) termcost(x, xsp, pars);
l = mpc.getCasadiFunc(stagecost_casadi, [Nx, Nu, Nx, Nu], {'x', 'u', 'xsp', 'usp'}, {'l'});
Vf = mpc.getCasadiFunc(termcost_casadi, [Nx, Nx], {'x', 'xsp'}, {'Vf'});

% Make NMPC controller.
Ncontrol = struct('x', Nx, 'u', Nu, 't', N);
values.xsp = xsp(:, 1:(N + 1));
values.usp = usp(:, 1:N);
guess.x = xsp(:, 1:(N+1));
guess.u = usp(:, 1:N);
Ncontrol.c = pars.colloc;

% Avoid using terminal constraint (use high terminal penalty instead so
% that ipopt can solve the problem).
solverNMPC = mpc.nmpc('f', ode_casadi, 'N', Ncontrol, 'Delta', Delta, ...
                      'verbosity', 0, 'l', l, 'Vf', Vf, ...
                      'x0', x0, 'guess', guess, 'par', values, ...
                      'lb', struct('x', xlb*ones(1, N + 1), 'u', ulb*ones(Nu, N)), ...
                      'ub', struct('x', xub*ones(1, N + 1), 'u', uub*ones(Nu, N)));

% Closed-loop simulation.
Nsim = tfinal/Delta;
x = NaN(Nx, Nsim + 1);
x(:, 1) = x0;
xplant = NaN(Nx, (plantSteps*Nsim + 1));
xplant(:, 1) = x0;
xplantnow = NaN(Nx, plantSteps + 1);
xplantnow(:, 1) = x0;
u = NaN(Nu, Nsim);

for i = 1:Nsim
    % Set initial condition and solve.
    solverNMPC.fixvar('x', 1, x(:, i));
    solverNMPC.par.xsp = xsp(:, i:(i + N));
    solverNMPC.par.usp = usp(:, i:(i + N - 1));
    solverNMPC.solve();

    % Print status.
    fprintf('%d: %s\n', i, solverNMPC.status);
    if ~isequal(solverNMPC.status, 'Solve_Succeeded')
        warning('Failed at time %d!', i);
        break
    end

    % Inject control and simulate plant using finer step size.
    u(:,i) = solverNMPC.var.u(:,1);
    for j = 1:plantSteps
        xplantnow(:, j+1) = full(cstrsim(xplantnow(:, j), u(:,i), 1));
    end
    xplant(:, 1 + (1:plantSteps) + (i-1)*plantSteps) = xplantnow(:, 2:end);
    xplantnow(:, 1) = xplantnow(:, end);
    x(:,i + 1) = xplantnow(:, end);
    solverNMPC.saveguess();
end

% Save data.
result = struct();
result.pars = rmfield(pars, 'ode');
result.x = x;
result.u = u;
result.t = (0:Delta:tfinal)';
result.xplant = xplant;
result.tplant = (0:(Delta/plantSteps):tfinal)';

end%function

function l = stagecost(x, u, xsp, usp, pars)
    % Quadratic stage cost.
    Q = pars.Q;
    R = pars.R;
    xerr = x(1:pars.Nx) - xsp(1:pars.Nx);
    uerr = u - usp;
    l = Q*(xerr'*xerr) + R*(uerr'*uerr);
end%function

function Vf = termcost(x, xsp, pars)
    % Quadratic terminal penalty.
    Qf = pars.Qf;
    xerr = x(1:pars.Nx) - xsp(1:pars.Nx);
    Vf = Qf*(xerr'*xerr);
end%function

cstrparam.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
function pars = cstrparam()
% Loads default parameters for robust MPC CSTR problem.

% Model Parameters.
pars = struct();
pars.theta = 20;
pars.k = 300;
pars.M = 5;
pars.xf = 0.3947;
pars.xc = 0.3816;
pars.alpha = 0.117;

% Simulation.
pars.tfinal = 300;
pars.N = 40;
pars.Q = 1/2;
pars.R = 1/2;
pars.Qf = 1e5;
pars.Nx = 2;
pars.Nu = 1;
pars.Np = 1;
pars.Delta = 3;
pars.xub = [2; 2];
pars.xlb = [0; 0];
pars.uub = 2;
pars.ulb = 0;
pars.colloc = 5;
pars.plantSteps = 2;

% Initial Conditions and Setpoints.
pars.x0 = [0.9831; 0.3918];
pars.ze = [0.2632; 0.6519];
pars.uprev = 0.02;
pars.usp = 455/600;

pars.uub_nominal = 2;
pars.ulb_nominal = 0.02;
pars.A = 0;
pars.w = 1;

pars.ode = @cstrode;

% Set the random number generator seed.
rand('state', 0);

end%function

function dxdt = cstrode(x, u, p, pars)
    % Nonlinear ODE model for reactor.

    c = x(1);
    T = x(2);
    t = x(3); % Augmented time state for time-varying model.

    rate = pars.k*c*exp(-pars.M/T);
    w = pars.A*sin(t*pars.w)*p;

    dcdt = (1 - c)/(pars.theta) - rate;
    dTdt = (pars.xf - T)/(pars.theta) + rate ...
           - pars.alpha*u*(T - pars.xc) + w;
    dtdt = 1;

    dxdt = [dcdt; dTdt; dtdt];
end%function

resample_nominal.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
function reftraj_resampled = resample_nominal(reftraj, Delta)
    % Resample the reference (central path) trajectory.

    t = reftraj.t;
    u = reftraj.u;
    x = reftraj.x;
    t0 = t(1);
    tf = t(end);
    tnew = (t0:Delta:tf)';

    % Interpolate to get new reference trajectories.
    unew = interp1(t(1:end-1), u', tnew, 'spline', 'extrap');
    xnew = interp1(t, x', tnew, 'spline', 'extrap');

    reftraj_resampled = struct();
    reftraj_resampled.t = tnew;
    reftraj_resampled.u = unew';
    reftraj_resampled.x = xnew';