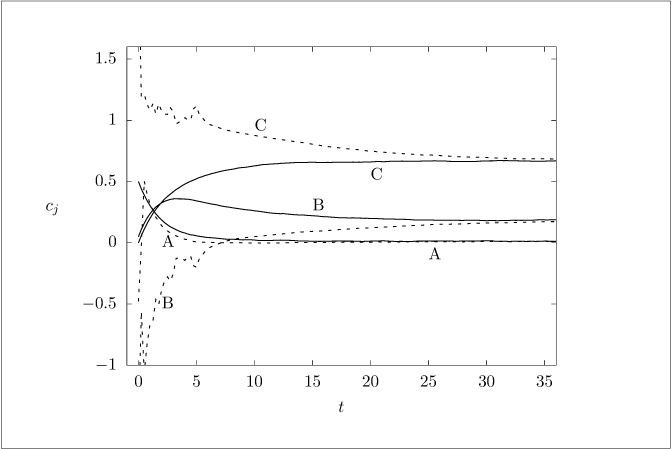
Figure 4.4

Code for Figure 4.4

main.m

% This file simulates the Batch Reactor Example (3.2.1) from Haseltine
% & Rawlings (2005) UKF is implemented to this example and it is shown that it
% fails when a poor prior is used.
data = struct();

% Helper functions.



% Simulate.
fprintf('Simulating without clipping.\n');
data.noclip = doukf(150, false());
fprintf('Simulating with clipping.\n');
data.yesclip = doukf(180, true());

batchreactor.m

function pars = batchreactor(Nsim)
% pars = batchreactor(Nsim)
%
% Returns a struct of batch reactor parameters to avoid duplication across
% MHE, EKF, and UKF scripts.
narginchk(1, 1);
mpc = import_mpctools();

% Sizes.
Delta = 0.25;
Nx = 3;
Ny = 1;
Nw = Nx;
Nv = Ny;

% Random variable standard deviations.
sig_v = 0.25; % Measurement noise.
sig_w = 0.001; % State noise.
sig_p = 0.5; % Prior.

P = sig_p.^2*eye(Nx);
Q = sig_w.^2*eye(Nw);
R = sig_v.^2*eye(Ny);

% Get model functions.
plant = mpc.getCasadiIntegrator(@batch_model, Delta, [Nx], {'x'});
frk4 = mpc.getCasadiFunc(@(x) batch_model(x), [Nx], {'x'}, {'frk4'}, ...
                         'rk4', true(), 'Delta', Delta, 'M', 4);
f = mpc.getCasadiFunc(@(x, w) frk4(x) + w, [Nx, Nw], {'x', 'w'}, {'f'});
h = mpc.getCasadiFunc(@measurement, [Nx], {'x'}, {'h'});

% Choose prior.
xhat0 = [1; 0; 4];
x0 = [0.5; 0.05; 0.0];

% Simulate the system to get data.
randn('state', 0);
w = sig_w*randn(Nw, Nsim);
v = sig_v*randn(Nv, Nsim + 1);

xsim = NaN(Nx, Nsim + 1);
xsim(:,1) = x0;

ysim = NaN(Ny, Nsim + 1);
yclean = NaN(Ny, Nsim + 1);

for t = 1:(Nsim + 1)
    xsim(:,t) = max(xsim(:,t), 0); % Make sure concentration is nonnegative.
    yclean(:,t) = full(h(xsim(:,t)));
    ysim(:,t) = yclean(:,t) + v(:,t);

    if t <= Nsim
        xsim(:,t + 1) = full(plant(xsim(:,t))) + w(:,t);
    end
end
t = (0:Nsim)*Delta;

% Get plotting function for convenience.
reactorplot = @reactorplot;

% Package everybody up. Note that this is a quick and dirty approach.
varnames = who();
pars = struct();
for i = 1:length(varnames);
    v = varnames{i};
    pars.(v) = eval(v);
end

end%function

function dxdt = batch_model(x)
    % Nonlinear ODE function.
    k1 = 0.5;
    km1 = 0.05;
    k2 = 0.2;
    km2 = 0.01;

    cA = x(1);
    cB = x(2);
    cC = x(3);

    rate1 = k1*cA - km1*cB*cC;
    rate2 = k2*cB.^2 - km2*cC;
    dxdt = [
        -rate1;
        rate1 - 2*rate2;
        rate1 + rate2;
    ];
end%function

function y = measurement(x)
    % Linear measurement function.
    RT = 0.0821*400;
    y = RT*sum(x);
end%function

function fig = reactorplot(x, xhat, y, yhat, yclean, Delta)
    % Make a plot of actual and estimated states.
    narginchk(6, 6);
    fig = figure();
    Nx = 3;
    Nt = size(x, 2) - 1;
    t = (0:Nt)*Delta;

    ax = subplot(2, 1, 2);
    hold('on');
    plot(t, yclean, '-k', 'DisplayName', 'Actual');
    plot(t, yclean, '--c', 'DisplayName', 'Measured');
    plot(t, yhat, 'ok', 'DisplayName', 'Estimated');
    ylabel('P');
    xlabel('t');
    legend('Location', 'EastOutside');
    set(ax, 'ylim', [10, 35]);

    ax = subplot(2, 1, 1);
    hold('on');
    colors = {'r', 'b', 'g'};
    names = {'A', 'B', 'C'};
    for i = 1:Nx
        plot(t, x(i,:) + 1e-10, ['-', colors{i}], 'DisplayName', ...
             sprintf('Actual C_%s', names{i}));
        plot(t, xhat(i,:) + 1e-10, ['o', colors{i}], 'DisplayName', ...
             sprintf('Estimated C_%s', names{i}));
    end
    xlabel('t');
    ylabel('c_i');
    legend('Location', 'EastOutside');
    set(ax, 'ylim', [-1, 1.5]);
end%function

get_sigma.m

function [x_sigma, w_sigma, v_sigma] = get_sigma(Pz, xhat, pars)
    % [x_sigma, w_sigma, v_sigma] = get_sigma(Pz, pars)
    %
    % Returns sigma points obtained from scaled sqrtm(Pz).
    narginchk(3, 3);

    % Make sure covariance is positive-definite.
    [Pzchol, okay] = chol(Pz);
    if okay ~= 0
        warning('Pz is not positive definite!');
    end

    % Select sigma points.
    sqrtPz = sqrtm((pars.Nz + pars.lambda)*Pz);
    zhat = [xhat; zeros(pars.Nw + pars.Nv, 1)];
    z_sigma = bsxfun(@plus, [zeros(pars.Nz, 1), sqrtPz, -sqrtPz], zhat);

    % Split into pieces.
    x_sigma = z_sigma(1:pars.Nx,:);
    w_sigma = z_sigma(pars.Nx + (1:pars.Nw),:);
    v_sigma = z_sigma(pars.Nx + pars.Nw + (1:pars.Nv),:);

ukf_scale.m

function [x_sigma, weights] = ukf_scale(x_sigma, pars)
    % [x_sigma, weights] = ukf_scale(x_sigma, pars)
    %
    % Rescales the sigma points and adjusts weights so that each sigma point has
    % no negative components.
    %
    % x_sigma should be a matrix of column vectors with the first vector giving
    % the central point (which must always be feasible).
    x_center = x_sigma(:,1); % Central point.
    x_outer = x_sigma(:,2:end);

    % Choose theta to make each point feasible.
    dx = abs(bsxfun(@minus, x_outer, x_center));
    err = abs(min(x_outer, 0)); % Gets negative part.
    err(x_center < 0,:) = 0; % Can't fix indices where x_center is negative.
    dx(err == 0) = 1; % Avoid division by zero.
    theta = 1 - max(err./dx);

    % Rescale outer points.
    x_outer = bsxfun(@times, theta, x_outer) ...
              + bsxfun(@times, 1 - theta, x_center);
    x_sigma = [x_center, x_outer];

    % Calculate weights.
    rho = (2*pars.lambda - 1)/(pars.Nsigma - sum(theta));
    a = -rho/(2*(pars.Nz + pars.lambda));
    b = (1 + rho)/(2*(pars.Nz + pars.lambda));
    weights = [0, a*theta]' + b;

doukf.m

function data = doukf(Nsim, clipping)
    % data = doukf(Nsim, clipping)
    %
    % Simulate the UKF with or without clipping.
    pars = batchreactor(Nsim);
    Nx = pars.Nx;
    Ny = pars.Ny;
    Nw = pars.Nw;
    Nv = pars.Nv;
    pars.Nz = Nx + Nw + Nv; % Augmented state is z = [x; w; v].
    Nz = pars.Nz;

    % Choose simulation parameters.
    Nsim = pars.Nsim;
    t = pars.t;
    x = pars.xsim;
    y = pars.ysim;
    Px = pars.P;
    Qw = pars.Q;
    Rv = pars.R;

    % Choose UKF weights.
    Nsigma = 1 + 2*Nz;
    pars.Nsigma = Nsigma;
    pars.lambda = 1; % From Vachhani et. al. (2006). Guarantees Pz > 0.
    pars.weights = [2*pars.lambda; ones(2*Nz, 1)]/(2*(Nz + pars.lambda));
    W = diag(pars.weights);

    % Preallocate variables.
    xhat = NaN(Nx, Nsim + 1);
    yhat = NaN(Ny, Nsim + 1);
    e = NaN(Ny, Nsim + 1);

    xhat(:,1) = pars.xhat0; % Poor initial guess
    zhat(1:Nx,1) = pars.xhat0;

    Pz = blkdiag(Px, Qw, Rv); % Covariance for extended state.
    [x_sigma, w_sigma, v_sigma] = get_sigma(Pz, xhat(:,1), pars);

    for t = 1:(Nsim + 1)
        % Take measurement.
        y_sigma = NaN(Ny, Nsigma);
        for i = 1:Nsigma
            y_sigma(:,i) = full(pars.h(x_sigma(:,i))) + v_sigma(:,i);
        end
        yhat(:,t) = y_sigma*pars.weights;
        e(:,t) = y(:,t) - yhat(:,t);

        % Apply correction.
        Ex = bsxfun(@minus, x_sigma, xhat(:,t));
        Ey = bsxfun(@minus, y_sigma, yhat(:,t));

        Exy = Ex*W*Ey';
        Eyy = Ey*W*Ey';

        L = Exy/Eyy;

        Px = Px - L*Exy';
        xhat(:,t) = xhat(:,t) + L*e(:,t);

        % Stop if at end of simulation.
        if t > Nsim
            break
        end

        % Calculate new sigma points, and clip if necessary.
        Pz = blkdiag(Px, Qw, Rv);
        [x_sigma, w_sigma, v_sigma] = get_sigma(Pz, xhat(:,t), pars);
        if clipping
            [x_sigma, pars.weights] = ukf_scale(x_sigma, pars);
        end

        % Simulate sigma points and calculate new xhat and Px.
        for i = 1:Nsigma
            x_sigma(:,i) = full(pars.f(x_sigma(:,i), w_sigma(:,i)));
        end
        xhat(:,t + 1) = x_sigma*pars.weights;
        Ex = bsxfun(@minus, x_sigma, xhat(:,t + 1));
        Px = Ex*W*Ex';
    end

    % Make a plot.
    pars.reactorplot(x, xhat, y, yhat, pars.yclean, pars.Delta);
    set(gca(), 'ylim', [-1, 1.5]);

    % Form data table.
    data = [pars.t', x', xhat', y', yhat'];

Figure 4.4:

Evolution of the state (solid line) and UKF state estimate (dashed line).

Code for Figure 4.4

main.m

batchreactor.m

get_sigma.m

ukf_scale.m

doukf.m