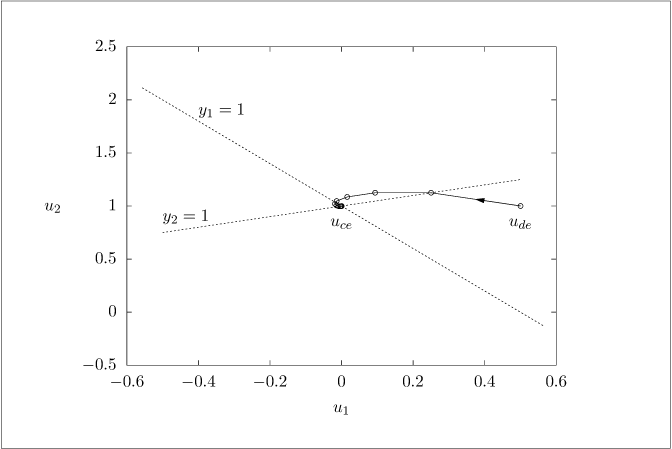
Figure 6.4:

Ten iterations of noncooperative steady-state calculation; reversed pairing.

Code for Figure 6.4

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
% A 2-variable steady-state problem.
lams = {[0.5, 0.5], [0.2, 0.8], [0.8, 0.2], [0.5, 0.5]};
iters = [10, 25, 25, 25];
names = {'equal', 'first', 'second', 'swapped'};
swaps = [false(), false(), false(), true()];


% Simulate with different values of lambda.
data = struct();
for i = 1:length(lams)
    data.(names{i}) = noncoopvscoop(lams{i}, iters(i), names{i}, swaps(i));
end

noncoopvscoop.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
function data = noncoopvscoop(lam, Niter, name, swap)
    % Simulates non-cooperative vs. cooperative optimization.
    narginchk(3, 4);
    if nargin() < 4
        swap = false();
    end

    % Unstable for about m1 < 0.58, lam1 = lam2 = 0.5.
    m1 = 0.5;
    m2 = -1/m1;
    g  = [-m1, 1; -m2, 1];
    if swap
        g = [0, 1; 1, 0]*g;
    end

    ysp = [1; 1];
    usp = g\ysp;
    ude = [ysp(1)/g(1,1); ysp(2)/g(2,2)];

    % Noncooperative problem.
    Lnc = [1-lam(1), -lam(1)*g(1,2)/g(1,1); -lam(2)*g(2,1)/g(2,2), 1-lam(2)];
    Knc = diag([lam(1)/g(1,1), lam(2)/g(2,2)]);

    ssnc = abs(eig(Lnc));

    unc = zeros(2, Niter + 1);
    unc(:,1) = ude;

    for i = 1:Niter
        unc(:,i+1) = Knc*ysp + Lnc*unc(:,i);
    end

    % Cooperative problem.
    Q = diag(lam);
    H = [Q, zeros(2,1); zeros(1,2), 0];
    G1 = g(:,1); G2 = g(:,2);
    D = [eye(2), -G1];
    M = [H, -D'; -D, zeros(2)];
    Minv = inv(M);
    K1 = Minv(3,1:2)*Q;
    L1 = -Minv(3,4:5)*G2;
    D = [eye(2), -G2];
    M = [H, -D'; -D, zeros(2)];
    Minv = inv(M);
    K2 = Minv(3,1:2)*Q;
    L2 = -Minv(3,4:5)*G1;
    Kco = [lam(1)*K1; lam(2)*K2];
    Lco = [(1-lam(1)), lam(1)*L1; lam(2)*L2, (1-lam(2))];
    ssco = abs(eig(Lco));

    uco = zeros(2, Niter);
    uco(:,1) = ude;

    for i = 1:Niter
       uco(:,i+1) = Kco*ysp + Lco*uco(:,i);
    end

    % Make lines for plotting.
    ld = min(unc');
    ru = max(unc');
    lr = max(-ld(1), ru(1));
    ud = max(-ld(2), ru(2));
    sslines = [-lr, lr, NaN(), -ud/m2, ud/m2;
               -m1*lr, m1*lr, NaN(), -ud, ud];
    sslines = sslines + repmat(usp, 1, 5);

    % Make plot.
    figure();
    plot(sslines(1,:), sslines(2,:), '-k', ...
         unc(1,:), unc(2,:), '-sr', ...
         uco(1,:), uco(2,:), '-og');
    title(sprintf('%s (lambda = [%g, %g])', name, lam));
    legend('Steady State', 'Non-cooperative', 'Cooperative');
    xlabel('u_1');
    ylabel('u_2');

    % Package data.
    data = struct('ss', sslines', 'noncoop', unc', 'coop', uco');