Figure 6.7:

Cost contours for a two-player, nonconvex game.

Code for Figure 6.7

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
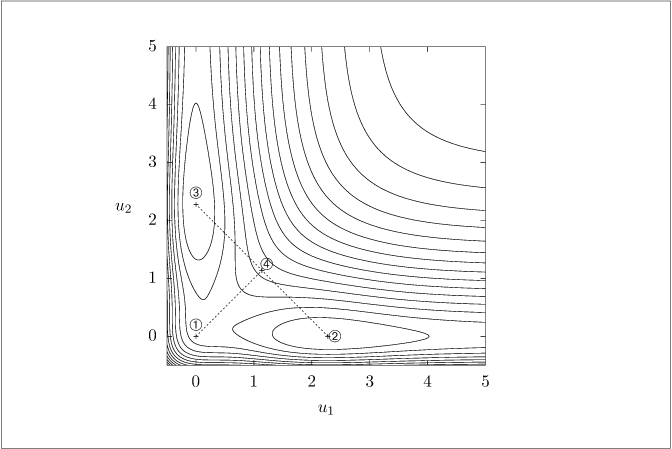
% Example of nonconvex optmization in which the convex combination of
% one-variable-at-a-time optimizations is not decreasing.

nxy = 221;
xvec = linspace(-0.5, 5, nxy);
yvec = linspace(-0.5, 5, nxy);
ncont = 15;


[xgrid, ygrid] = meshgrid(xvec, yvec);
Vgrid = V(xgrid, ygrid);

% choose initial point and find the two one variable at a time
% minimizers.
x0 = 0;
y0 = 0;

xguess = 2.5;
yguess = 2.5;

xp = fminsearch(@(x) V(x, y0), xguess);
yp = fminsearch(@(y) V(x0, y), yguess);

xw = (x0 + xp)/2;
yw = (y0 + yp)/2;

figure();
hold('on');
c = contour(xvec, yvec, Vgrid, ncont);
plot(x0, x0, 'ok', xp, y0, '+k', x0, yp, '+k', xw, yw, 'ok', ...
     [xp, x0], [y0, yp], '-k', [x0, xw], [x0, yw], '-k')

V.m

1
2
3
4
5
function retval = V(x, y)
    a = 1.1;
    b = 0.4;
    retval = exp(-2*x) - 2*exp(-x) + exp(-2*y) - 2*exp(-y) ...
             + a*exp(-b*((x + 0.2).^2 + (y + 0.2).^2));