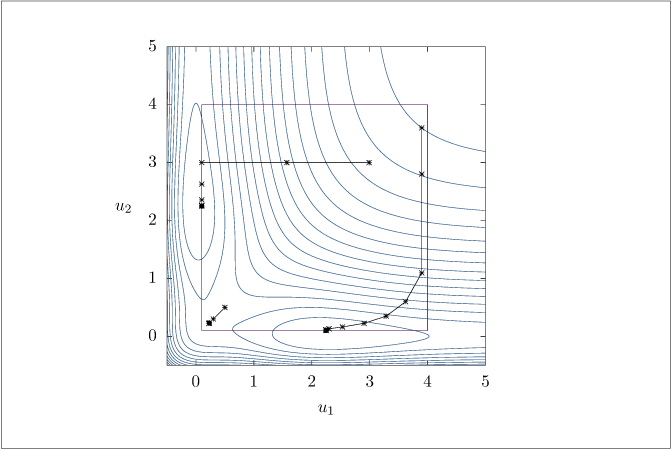
Figure 6.8:

Nonconvex function optimized with the distributed gradient algorithm.

Code for Figure 6.8

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
% Example of nonconvex optmization using cooperative optimization.
nxy = 221;
xvec = linspace(-0.5, 5, nxy);
yvec = linspace(-0.5, 5, nxy);
ncont = 15;


[xgrid, ygrid] = meshgrid(xvec, yvec);
Vgrid = V(xgrid, ygrid);

Vfunc = @(u) V(u(1), u(2));

% Run distributed optimization for different initial conditions.
ulb = 0.1*[1; 1];
uub = 4*[1; 1];
U = [uub(1), ulb(1), ulb(1), uub(1), uub(1);
     uub(2), uub(2), ulb(1), ulb(1), uub(2)];

Nu = 2;
u0s = [0.5, 0.5; 3.9, 3.6; 2.99, 3]';
Nu0 = size(u0s, 2);
uiter = cell(Nu0, 1);
for i = 1:Nu0
    [~, uiter{i}] = distributedgradient(Vfunc, u0s(:,i), ulb, uub);
end

% Make a plot.
figure();
hold('on');
c = contour(xvec, yvec, Vgrid, ncont);
plot(U(1,:), U(2,:), '-k');
markers = 'os^<>v';
for i = 1:Nu0
    plot(uiter{i}(1,:), uiter{i}(2,:), ['-', markers(i), 'k']);
end

distributedgradient.m

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
function [ustar, uiter] = distributedgradient(V, u0, ulb, uub, varargin)
% [ustar, uiter] = distributedgradient(V, u0, ulb, uub, ...)
%
% Runs a distributed gradient algorithm for a problem with box constraints.
%
% V should be a function handle defining the objective function. u0 should be
% the starting point. ulb and uub should give the box constraints for u.
%
% Additional arguments are passed as 'key' value pairs. They are as follows:
%
% - 'beta', 'sigma' : parameters for line search (default 0.8 and 0.01)
% - 'alphamax' : maximum step to take in any iteration (default 10)
% - 'Niter' : Maximum number of iterations (default 25)
% - 'steptol', 'gradtol' : Absolute tolerances on stepsize and gradient.
%                          Algorithm terminates if the stepsize is less than
%                          steptol and the gradient is less than gradtol
%                          (defaults 1e-5 and 1e-6). Set either to a negative
%                          value to never stop early.
% - 'Nlinesearch' : maximum number of backtracking steps (default 100)
% - 'I' : cell array defining the variables for each system. Default is
%         each variable is a separate system.
%
% Return values are ustar, the final point, and uiter, a matrix of iteration
% progress.
narginchk(4, inf());

% Get options.
param = struct('beta', 0.8, 'sigma', 0.01, 'alphamax', 15, 'Niter', 50, ...
               'steptol', 1e-5, 'gradtol', 1e-6, 'Nlinesearch', 100, ...
               'I', []);
for i = 1:2:length(varargin)
    param.(varargin{i}) = varargin{i + 1};
end
Nu = length(u0);
if isempty(param.I)
    param.I = num2cell((1:Nu)');
end

% Project initial condition to the feasible space.
u0 = min(max(u0, ulb), uub);

% Get gradient function via CasADi.
usym = casadi.SX.sym('u', Nu);
vsym = V(usym);
Jsym = jacobian(vsym,usym);
dVcasadi = casadi.Function('V', {usym}, {Jsym, vsym});

% Start the loop.
k = 1;
uiter = NaN(Nu, param.Niter + 1);
uiter(:,1) = u0;
[g, gred] = calcgrad(dVcasadi, u0, ulb, uub);
v = inf(Nu, 1);
while k <= param.Niter && (norm(gred) > param.gradtol || norm(v) > param.steptol)
    % Take step.
    [uiter(:,k + 1), v] = coopstep(param.I, V, g, uiter(:,k), ulb, uub, param);
    k = k + 1;

    % Update gradient.
    [g, gred] = calcgrad(dVcasadi, uiter(:,k), ulb, uub);
end

% Get final point and strip off any extra points in uiter.
uiter = uiter(:,1:k);
ustar = uiter(:,end);

end%function

function [u, v] = coopstep(I, V, g, u0, ulb, uub, param)
    % [u, v] = coopstep(I, V, g, u0, ulb, uub, param)
    %
    % Takes one step of cooperative distributed gradient projection subject
    % to box constraints on u.
    %
    % I should be the cell array of partitions. V should be the function handle
    % and g its gradient at u0.
    narginchk(7, 7);
    Nu = length(u0);
    Ni = length(I);
    us = NaN(Nu, Ni);
    Vs = NaN(1, Ni);

    % Run each optimization.
    V0 = V(u0);
    for j = 1:Ni
        % Compute step.
        v = zeros(Nu, 1);
        i = I{j};
        v(i) = -g(i);
        ubar = min(max(u0 + v, ulb), uub);
        v = ubar - u0;

        % Choose alpha.
        if any(ubar == ulb) || any(ubar == uub)
            alpha = 1;
        else
            alpha = [(ulb(i) - u0(i))./v(i); (uub(i) - u0(i))./v(i)];
            alpha = min(alpha(alpha >= 0));
            if isempty(alpha)
                alpha = 0; % Nowhere to go. Possibly at a stationary point.
            else
                alpha = min(alpha, param.alphamax); % Don't step too far.
            end
        end

        % Backtracking line search.
        k = 1;
        while V(u0 + alpha*v) > V0 + param.sigma*alpha*(g(i)'*v(i)) ...
                && k <= param.Nlinesearch
            alpha = param.beta*alpha;
            k = k + 1;
        end
        us(:,j) = u0 + alpha*v;
        Vs(j) = V(us(:,j));
    end

    % Choose step to take.
    w = ones(Ni, 1)/Ni;
    for j = 1:Ni
        % Check for descent.
        u = us*w;
        if V(u) <= Vs*w
            break
        elseif j == Ni
            u = u0;
            warning('No descent directions!');
            break
        end

        % Get rid of worst player.
        [~, jmax] = max(Vs);
        Vs(jmax) = -realmax(); % Exclude from later steps.
        w(jmax) = 0;
        w = w/sum(w);
    end

    % Calculate actual step.
    v = u - u0;
end%function

function [g, gred] = calcgrad(dV, u, ulb, uub)
    % Calculates the gradient and reduced gradient at a given point.
    narginchk(4, 4);
    g = full(dV(u));
    g = g(:); % Column vector.
    gred = g;
    gred((u == ulb) & (g > 0)) = 0;
    gred((u == uub) & (g < 0)) = 0;
end%function

V.m

1
2
3
4
5
function retval = V(x, y)
    a = 1.1;
    b = 0.4;
    retval = exp(-2*x) - 2*exp(-x) + exp(-2*y) - 2*exp(-y) ...
             + a*exp(-b*((x + 0.2).^2 + (y + 0.2).^2));