Figure 8.10

% Simulates a system using Gauss-Legendre collocation schemes of order 2, 4 and 6
% Joel Andersson, UW Madison 2017

% Declare model variables
x1 = casadi.SX.sym('x1');
x2 = casadi.SX.sym('x2');
u = casadi.SX.sym('u');

% Model equations
x1_dot = (1-x2^2)*x1 - x2 + u;
x2_dot = x1;

% Objective function (integral term)
quad = x1^2 + x2^2 + u^2;

% Dimensions
nx = 2;
np = 1;

% Test value
x_test = [0; 1];
u_test = 0.5;

% End time
T = 10;

% Nunber of integrator steps
N = 20;

% Time step
dt = T/N;

% Time grid for plotting
tgrid = linspace(0, T, N+1);

% Simulate with collocation, order 1, 2 and 3
for d=[1,2,3]
  % Gauss-Legendre points
  switch d
    case 1
      tau_root = [0, 0.5];
    case 2
      tau_root = [0, 0.5-sqrt(3)/6, 0.5+sqrt(3)/6];
    case 3
      tau_root = [0, 0.5-sqrt(15)/10, 0.5, 0.5+sqrt(15)/10];
    otherwise
      error('order not supported');
   end

   % Degree of interpolating polynomial
   d = numel(tau_root)-1;

   % Coefficients of the collocation equation
   C = zeros(d+1,d+1);

   % Coefficients of the continuity equation
   D = zeros(d+1, 1);

   % Coefficients of the quadrature function
   B = zeros(d+1, 1);

   % Construct polynomial basis
   for j=1:d+1
     % Construct Lagrange polynomials to get the polynomial basis at the collocation point
     coeff = 1;
     for r=1:d+1
       if r ~= j
         coeff = conv(coeff, [1, -tau_root(r)]);
         coeff = coeff / (tau_root(j)-tau_root(r));
       end
     end
     % Evaluate the polynomial at the final time to get the coefficients of the continuity equation
     D(j) = polyval(coeff, 1.0);

     % Evaluate the time derivative of the polynomial at all collocation points to get the coefficients of the continuity equation
     pder = polyder(coeff);
     for r=1:d+1
       C(j,r) = polyval(pder, tau_root(r));
     end

     % Evaluate the integral of the polynomial to get the coefficients of the quadrature function
     pint = polyint(coeff);
     B(j) = polyval(pint, 1.0);
   end

   % Continuous-time dynamics
   f = casadi.Function('f', {[x1;x2], u}, {[x1_dot;x2_dot], quad},...
                {'x','p'}, {'ode','quad'});

   % Start with an empty nonlinear system of equations
   w = {};
   w0 = {}; % guess for w
   rhs = {};

   % x0, p are parameters of the Newton solver
   X0 = casadi.MX.sym('X0', nx);
   P = casadi.MX.sym('P', np);

   % State vector at collocation points are unknowns
   Xj = cell(1,d);
   for j=1:d
      Xj{j} = casadi.MX.sym(['X_' num2str(j)], nx);
      w{end+1} = Xj{j};
      w0{end+1} = zeros(nx,1);
   end

   % Get expressions for the state derivatives at all collocation points
   % from differentiating the polynomials
   Xj_dot = cell(1,d);
   for j=1:d
       Xj_dot{j} = C(1,j+1)*X0;
       for r=1:d
          Xj_dot{j} = Xj_dot{j} + C(r+1,j+1)*Xj{r};
       end
   end

   % Evaluate the function at all the collocation points
   ode_j = cell(1,d);
   quad_j = cell(1,d);
   for j=1:d
       [ode_j{j}, quad_j{j}] = f(Xj{j}, P);
   end

   % Gather collocation equations
   for j=1:d
       rhs{end+1} = dt*ode_j{j} - Xj_dot{j};
   end

   % Get an expression for the state at the end of the interval
   Xf = D(1)*X0;
   for j=1:d
       Xf = Xf + D(j+1)*Xj{j};
   end

   % Get an expression for the quadrature
   Qf = 0;
   for j=1:d
       Qf = Qf + B(j+1)*quad_j{j}*dt;
   end

   % Concatenate nonlinear equations and variables
   w = vertcat(w{:});
   w0 = vertcat(w0{:});
   rhs = vertcat(rhs{:});

   % Create a rootfinding solver object
   rfp = casadi.Function('rfp', {w, X0, P}, {rhs, Xf, Qf},...
                        {'w0', 'x0', 'p'}, {'w', 'xf', 'qf'});
   solver = casadi.rootfinder('solver', 'newton', rfp);

   % Simulate
   x_sim = x_test;
   q_sim = 0;
   w_sim = w0;
   for k=1:N
     sol = solver('x0', x_sim(:, end), 'p', u_test, 'w0', w_sim);
     x_sim = [x_sim, full(sol.xf)];
     q_sim = [q_sim, q_sim(:,end) + full(sol.qf)];
     w_sim = sol.w;
   end
   switch d
     case 1
       x_gl2 = x_sim;
       q_gl2 = q_sim;
    case 2
       x_gl4 = x_sim;
       q_gl4 = q_sim;
    case 3
       x_gl6 = x_sim;
       q_gl6 = q_sim;
    otherwise
      error('order not supported');
   end
end

% Compare with CVODES with high accuracy
prob = struct('x', [x1;x2], 'p', u, 'ode', [x1_dot;x2_dot], 'quad', quad);
opts = struct('grid', tgrid, 'output_t0', true, 'reltol', 1e-13, 'abstol', 1e-13);
integ = casadi.integrator('integ', 'cvodes', prob, opts);
sol = integ('x0', x_test, 'p', u_test);
x_cvodes = full(sol.xf);
q_cvodes = full(sol.qf);

% Plot the solution
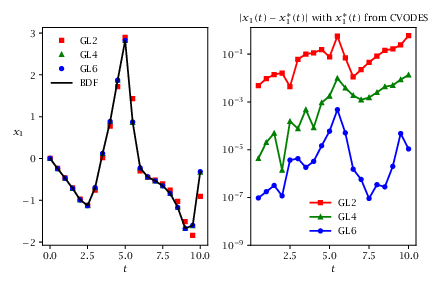
figure();
clf;

% Plot x_1(t)
subplot(1,2,1)
hold on;
grid on;
plot(tgrid, x_gl2(1,:), 'r*-');
plot(tgrid, x_gl4(1,:), 'gx-');
plot(tgrid, x_gl6(1,:), 'bo-');
plot(tgrid, x_cvodes(1,:), 'k-');
xlabel('t')
title('Simulation x_1(t)')
legend('GL2', 'GL4', 'GL6', 'BDF', 'Location', 'northwest')

% Plot error
subplot(1,2,2)
hold on;
grid on;
semilogy(tgrid(2:end), abs(x_gl2(1,2:end)-x_cvodes(1,2:end)), 'r*-');
semilogy(tgrid(2:end), abs(x_gl4(1,2:end)-x_cvodes(1,2:end)), 'gx-');
semilogy(tgrid(2:end), abs(x_gl6(1,2:end)-x_cvodes(1,2:end)), 'bo-');
xlabel('t')
title('|x_1(t) - x^*_1(t)| with x^*_1(t) from CVODES')
legend('GL2','GL4','GL6','Location', 'south')
Figure 8.10:

Open-loop simulation for (8.65) using collocation.

Code for Figure 8.10

main.m
