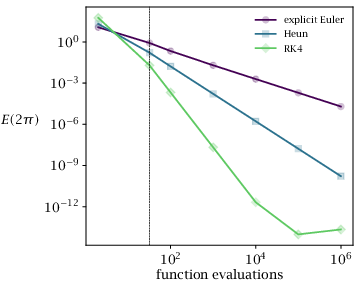
Figure 8.2(a):

Performance of different integration methods. Accuracy vs. function evaluations.

Code for Figure 8.2(a)

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
% Accuracy of explicit numerical integration of a linear ODE.

% Butcher tableaus (only a and b) for the three methods.
tabs = struct();
tabs.euler = struct('a', 0, 'b', 1);
tabs.heun = struct('a', [0, 0; 1, 0], 'b', [0.5, 0.5]);
tabs.rk4 = struct('a', [0, 0, 0, 0; 0.5, 0, 0, 0; 0, 0.5, 0, 0; 0, 0, 1, 0], ...
                  'b', [1/6, 1/3, 1/3, 1/6]);
tabnames = fieldnames(tabs);

% Run each method.
A = [0, 1; -1, 0];
f = @(x) A*x;
x0 = [1; 0];

% Choose values of M to test. Note that the figure in the text goes up to
% M = 10^6, which takes about an hour to run.
Ms = [2, 32, 1e2, 1e3, 1e4];
err = struct();
for n = 1:length(tabnames)
    n = tabnames{n};
    err.(n) = NaN(size(Ms));
    fprintf('Running %s.\n', n);
    for i = 1:length(Ms)
        M = Ms(i);
        fprintf('  M = %d\n', M);
        a = tabs.(n).a;
        b = tabs.(n).b;
        N = ceil(M/length(b)); % Number of integration steps.
        h = 2*pi()/N;
        x = x0;
        for t = 1:N
            x = butcherintegration(x, f, h, a, b);
        end
        err.(n)(i) = norm(x - x0);
    end
end

% Make a plot.
figure();
hold('on');
colors = {'r', 'g', 'b'};
for n = 1:length(tabnames)
    c = colors{n};
    n = tabnames{n};
    loglog(Ms, err.(n), ['-o', c], 'displayname', n);
end
xlabel('collocation points M');
ylabel('Error');
legend('location', 'northwest');

butcherintegration.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
function [xplus, converged, iter, k] = butcherintegration(x, func, h, a, b, Niter)
% [xplus, converged, iter, k] = butcherintegration(x, f, h, a, b, [Niter=100])
%
% Performs numerical integration of f starting from x for h time units.
%
% f must be a function handle that returns dx/dt. If a defines an implicit
% method, then f must also return the Jacobian of dx/dt. In either case, f must
% be time-invariant.
%
% a and b should be the coefficients from the Butcher tableau for the
% integration scheme. If the a matrix defines an explicit scheme (i.e., zero on
% and above the diagonal, then the explicit formulas will be used. Otherwise,
% the implicit equations are solved using Newton's method.
%
% Niter is the maximum number of iterations to perform. xguess is a guess for
% x at the next timestep.
narginchk(5, 6);
if nargin() < 6
    Niter = 100;
end

% Check arguments.
x = x(:);
Nx = length(x);
b = h*b(:);
Ns = length(b);
if ~isequal(size(a), [Ns, Ns])
    error('a must be a square matrix with a column for each element of b!');
end
a = h*a;

% Decide if tableau is explicit or not.
if nnz(triu(a)) == 0
    k = butcher_explicit(x, func, a);
    converged = true();
    iter = 0;
else
    [k, converged, iter] = butcher_implicit(x, func, a, Niter);
end

% Advance state.
xplus = x + k*b;

end%function

% *****************************************************************************

function k = butcher_explicit(x, func, a)
% Performs an explicit integration step.
Nx = length(x);
Ns = size(a, 1);
k = zeros(Nx, Ns);
for i = 1:Ns
    k(:,i) = func(x + k*a(i,:)');
end
end%function

% *****************************************************************************

function [k, converged, iter] = butcher_implicit(x, func, a, Niter)
% Solves implicit integration using Newton's Method. Timestep is assumed 1.
narginchk(4, 4);
Nx = length(x);
Ns = size(a, 1);;
k = zeros(Nx, Ns);
converged = false();
iter = 0;
while ~converged && iter < Niter
    iter = iter + 1;

    dX = k*a';
    if Ns == 1
        [f, J] = func(x + dX);
        J = a*J;
    else
        f = zeros(Nx*Ns, 1);
        J = zeros(Nx*Ns, Nx*Ns);
        for i = 1:Ns
            I = ((i - 1)*Nx + 1):(i*Nx);
            [f(I), Ji] = func(x + dX(:,i));
            J(I,:) = kron(a(i,:), Ji);
        end
    end

    f = f - k(:);
    J = J - eye(Nx*Ns);
    dk = -J\f;
    k = k + reshape(dk, [Nx, Ns]);

    converged = norm(dk) < 1e-8;
end

end%function