Figure 8.5:

Newton-type iterations for solution of R(z)=0 from Example8.5. Left: exact Newton method. Right: constant Jacobian approximation.

Code for Figure 8.5

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
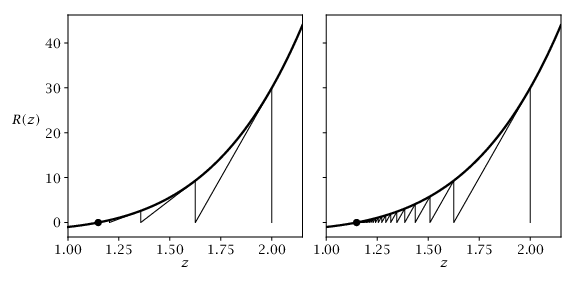
% Generate figure for Example 8.5.
% Adapted by tja from a script writen by someone in mmd's group, July 2017.

z0     = 2;      % Initial guess.
Mk     = 5*z0^4; % Inexact jacobian.
iter1  = 10;      % Number of iterations for exact Jacobian solver.
iter2  = 100;    % Number of iterations for exact Jacobian solver.
tol    = 1.0e-8; % Tolerance for solution.

% Preallocate and initialize.
% Exact Jacobian.
zk1 = zeros(iter1 + 1, 1);
zk1(1) = z0;
dashline1 = zeros(2*iter1 + 1, 2);
dashline1(1, :) = [z0, 0];
% Inexact Jacobian.
zk2 = zeros(iter2 + 1, 1);
zk2(1) = z0;
dashline2 = zeros(2*iter2 + 1, 2);
dashline2(1, :) = [z0, 0];

% Solve R(z) = z^5 - 2 with exact Jacobian Newton-type solver.
for i = 1:iter1
    zk1(i + 1) = zk1(i) - (5*zk1(i)^4) \ (zk1(i)^5 - 2);
    dashline1(2*i, :) = [zk1(i), zk1(i)^5 - 2] ;
    dashline1(2*i + 1, :) = [zk1(i + 1), 0];
end

% Solve R(z) = z^5 - 2 with inexact Jacobian Newton-type solver.
for i = 1:iter2
    zk2(i + 1) = zk2(i) - Mk \ (zk2(i)^5 - 2);
    dashline2(2*i, :) = [zk2(i), zk2(i)^5 - 2];
    dashline2(2*i + 1, :) = [zk2(i + 1), 0];
end

ztrue = 2^(1/5); % Exact solution.

z = 1 : 0.01 : 2.15;
R = z.^5 - 2;
figure();
subplot(1, 2, 1) % Exact Jacobian.
hold()
plot(z, R, 'k-') % Plot function.
plot(zk1, zeros(iter1 + 1, 1), 'o', 'markeredgecolor', 'k', ...
     'markerfacecolor', 'none') % Plot iterates along x axis as empty circles.
plot(ztrue, 0, 'o', 'markeredgecolor', 'k', ...
     'markerfacecolor', 'k') % Plot true solution as filled circle.
plot(dashline1(:, 1), dashline1(:, 2), '--k') % Plot dashed line.
xlabel('z')
ylabel('R(z)')
axis([z(1), z(end), R(1), R(end)])
box('on')

subplot(1, 2, 2) % Inexact Jacobian.
hold()
plot(z, R, 'k-') % Plot function.
plot(zk2, zeros(iter2 + 1, 1), 'o', 'markeredgecolor', 'k', ...
     'markerfacecolor', 'none') % Plot iterates along x axis as empty circles.
plot(ztrue, 0, 'o', 'markeredgecolor', 'k', ...
     'markerfacecolor', 'k') % Plot true solution as filled circle.
plot(dashline2(:, 1), dashline2(:, 2), '--k') % Plot dashed line.
xlabel('z')
ylabel('R(z)')
axis([z(1), z(end), R(1), R(end)])
box('on')

save -v7 Newton_Type_Solver.mat z R zk1 zk2 dashline1 dashline2 ztrue