Figure 8.7:

Relaxed and binary feasible solution for Example8.17.

Code for Figure 8.7

Text of the GNU GPL.

main.m

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
% Script to solve a small MINLP problem with a heuristic.

% Import MPCtools.
mpc = import_mpctools();

% Problem parameters.
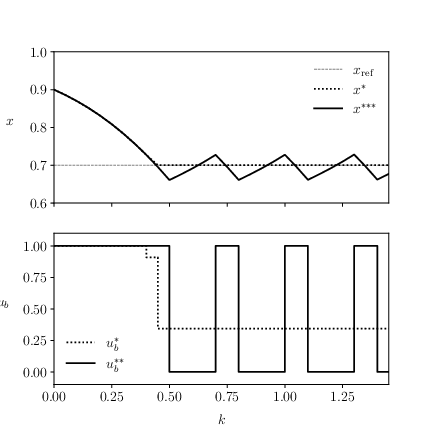
xref = 0.7;
Delta = 0.05;
x0 = 0.9;
Ncontroller = 30;
Nx = 1;
Nu = 1;
time = Delta*(0:29)';

% Functions for the NLP.
fxu = mpc.getCasadiFunc(@(x, u) x^3 - u, ...
                         [Nx, Nu], {'x', 'u'}, {'fxu'}, ...
                         'rk4', true(), 'Delta', Delta, 'M', 1);
lb = struct('u', 0);
ub = struct('u', 1);
N = struct('x', Nx, 'u', Nu, 't', Ncontroller);
l = mpc.getCasadiFunc(@(x) (x-xref)^2, ...
           [Nx], {'x'}, {'l'});
% Initial guess.
guess = struct();
guess.x = 0;
guess.u = 1;
% Gather everything to pass everything to MPC tools at once
kwargs = struct();
kwargs.N = N;
kwargs.x0 = x0;
kwargs.l = l;
kwargs.Vf = l;
kwargs.lb = lb;
kwargs.ub = ub;
kwargs.guess = guess;
% Controllers
nlp = mpc.nmpc('f', fxu, '**', kwargs);
nlp.solve();
unlp = nlp.var.u';
xnlp = nlp.var.x';
Vnlp = nlp.obj;

% Get the matrices that represent the constraints.
A = tril(ones(Ncontroller, Ncontroller));
B = zeros(Ncontroller, Ncontroller);
C = ones(Ncontroller, 1);
tempvec = [-1;1;-1];
for i=1:Ncontroller-2
  B(i:i+2, i) = tempvec;
end
B(Ncontroller-1:Ncontroller, Ncontroller-1) = [-1;1];
B(Ncontroller, Ncontroller) = -1;

% Setup and solve the MILP using bonmin.
eta = casadi.SX.sym('eta');
u = casadi.SX.sym('u', Ncontroller);
discrete = [false();repmat(true(), [Ncontroller, 1])];
ubg = [zeros(Ncontroller, 1);zeros(Ncontroller, 1);zeros(Ncontroller, 1)];
lbg = [-inf(Ncontroller, 1);-inf(Ncontroller, 1);-inf(Ncontroller, 1)];
milp = struct('x',[eta;u], 'f', eta, 'g', [A*u-A*unlp-C*eta;-A*u+A*unlp-C*eta;B*u;]);
nlpsol_obj = casadi.nlpsol('S', 'bonmin', milp, struct('discrete', discrete));
umilp = nlpsol_obj('x0', zeros(Ncontroller+1, 1), 'lbg', lbg, 'ubg', ubg);
maxcianorm = full(umilp.x(1));
umilp = full(umilp.x(2:end));

% Just simulate for the last step in the heuristic.
xopt = zeros(Ncontroller+1, 1);
xopt(1, 1) = x0;
for i=1:Ncontroller
  xopt(i+1, 1) = full(fxu(xopt(i, 1), umilp(i, 1)));
end

Vminlp = (xopt-xref)'*(xopt-xref);

% Save data.
save('-v7', 'CIA.mat', 'xref', 'time', 'xnlp', 'unlp', 'xopt', 'umilp');