1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
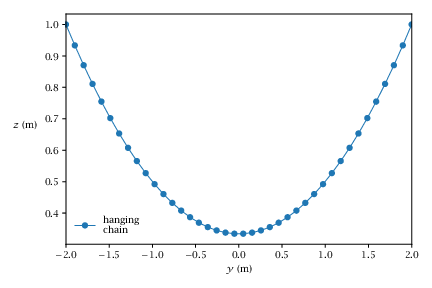
105 | % We want to model a chain attached to two supports and hanging in between. Let us discretise
% it with N mass points connected by N-1 springs. Each mass i has position (yi,zi), i=1,...,N.
% The equilibrium point of the system minimises the potential energy.
% The potential energy of each spring is
% Vi=D_i/2 * ((y_i-y_{i+1})^2 + (z_i-z_{i+1})^2)
% The gravitational potential energy of each mass is
% Vg_i = m_i*g0*z_i
% The total potential energy is thus given by:
% J(y_1,z_1,...,y_N,z_N) = 1/2*sum{i=1,...,N-1} D_i ((y_i-y_{i+1})^2+(z_i-z_{i+1})^2) + g0 * sum{i=1,...,N} m_i * z_i
%
% We wish to solve
% minimize{y(:),z(:)} J(...)
% Subject to the piecewise linear ground constraints:
% (1) z_i >= zin
% (2) z_i - 0.1*y_i >= 0.5
% The code below solves the unconstrained problem, without (1) and (2)
% Constants
N = 40;
m_i = 40.0/N;
D_i = 70.0*N;
g0 = 9.81;
% Objective function
J = 0;
% Start with an empty problem
x = {};
lbx = [];
ubx = [];
x0 = [];
g = {};
lbg = [];
ubg = [];
% Loop over all chain elements
for i=1:N
% Previous point
if i>1
y_prev = y_i;
z_prev = z_i;
end
% Create variables for the (y_i, z_i) coordinates
y_i = casadi.SX.sym(['y_',num2str(i)]);
z_i = casadi.SX.sym(['z_',num2str(i)]);
% Add variables to the problem formulation
x{end+1} = y_i;
x{end+1} = z_i;
% Add variable bounds
if i==1
% First mass fixed to (-2,1)
lbx = [lbx; -2; 1];
ubx = [ubx; -2; 1];
elseif i==N
% Last mass fixed to (2,1)
lbx = [lbx; 2; 1];
ubx = [ubx; 2; 1];
else
lbx = [lbx; -inf; -inf];
ubx = [ubx; inf; inf];
end
% Initial guess for the variables
x0 = [x0; 0; 0];
% Add (linear) constraints to the problem formulation
%g{end+1} = ...
% Add constraint bounds
%lbg = [lbg; ...];
%ubg = [ubg; ...];
% Spring potential
if i>1
J = J + D_i/2*((y_prev-y_i)^2 + (z_prev-z_i)^2);
end
% Graviational potential
J = J + g0 * m_i * z_i;
end
% Formulate QP
prob = struct('x', vertcat(x{:}), 'f', J, 'g', vertcat(g{:}));
% Solve with qpoases
solver = casadi.qpsol('solver', 'qpoases', prob);
% Get the optimal solution
sol = solver('lbx', lbx, 'ubx', ubx, 'lbg', lbg, 'ubg', ubg, 'x0', x0);
% Retrieve the result
x_opt = full(sol.x);
Y0 = x_opt(1:2:end);
Z0 = x_opt(2:2:end);
% Plot the result
plot(Y0,Z0,'o-')
xlabel('y [m]')
ylabel('z [m]')
title('Hanging chain QP')
grid on;
legend('Chain','location','southeast')
|