1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
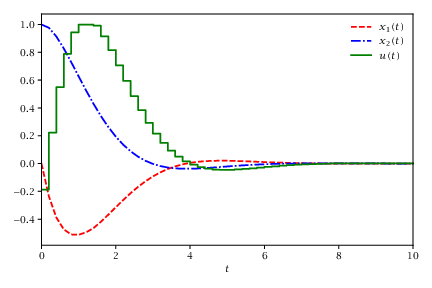
136 | % Solves the following minimization problem using direct single shooting
% minimize 1/2*integral{t=0 until t=T}(x1^2 + x2^2 + u^2) dt
% subject to dot(x1) = (1-x2^2)*x1 - x2 + u, x1(0)=0, x1(T)=0
% dot(x2) = x1, x2(0)=1, x2(T)=0
% with T=10
%
% This example can be found in CasADi's example collection in MATLAB/Octave,
% Python and C++ formats.
%
% Joel Andersson, UW Madison 2017
%
% States and control
x1 = casadi.SX.sym('x1');
x2 = casadi.SX.sym('x2');
u = casadi.SX.sym('u');
% Model equations
x1_dot = (1-x2^2)*x1 - x2 + u;
x2_dot = x1;
% Objective function (integral term)
quad = x1^2 + x2^2 + u^2;
% Define the problem structure
ocp = struct('x',[x1; x2],'u',u, 'ode', [x1_dot; x2_dot], 'quad',quad);
% Specify problem data
data = struct('T', 10,...
'x0', [0; 1],...
'xN', [ 0; 0],...
'u_min', -1,...
'u_max', 1,...
'u_guess', 0);
% Specify solver options
opts = struct('N', 50,...
'verbose', true);
% Problem independent code from here on
% Problem dimensions
N = opts.N;
nx = numel(ocp.x);
nu = numel(ocp.u);
% Time grid
tgrid = linspace(0, data.T, N+1);
% Continuous-time dynamics as a function
f = casadi.Function('f', {ocp.x, ocp.u}, {ocp.ode, ocp.quad}, ...
{'x','p'}, {'ode', 'quad'});
% RK4 integrator that takes a single step
dt = data.T / N;
x0 = casadi.MX.sym('x0', nx);
p = casadi.MX.sym('p', nu);
[k1, k1q] = f(x0, p);
[k2, k2q] = f(x0 + dt/2*k1, p);
[k3, k3q] = f(x0 + dt/2*k2, p);
[k4, k4q] = f(x0 + dt*k3, p);
xf = x0 + dt*(k1 + 2*k2 + 2*k3 + k4 )/6;
qf = dt*(k1q + 2*k2q + 2*k3q + k4q)/6;
F = casadi.Function('RK4', {x0, p}, {xf, qf}, ...
{'x0','p'}, {'xf', 'qf'});
% Start with an empty NLP
w = {}; % Variables
lbw = {}; % Lower bound on w
ubw = {}; % Upper bound on w
w0 = {}; % Initial guess for w
g = {}; % Equality constraints
J = 0; % Objective function
% Expressions corresponding to the trajectories we want to plot
x_plot = {};
u_plot = {};
% Initial conditions
xk = data.x0;
x_plot{end+1} = xk;
% Loop over all times
for k=0:N-1
% Declare local control
uk = casadi.MX.sym(['u' num2str(k)], nu);
w{end+1} = uk;
lbw{end+1} = data.u_min;
ubw{end+1} = data.u_max;
w0{end+1} = data.u_guess;
u_plot{end+1} = uk;
% Simulate the system forward in time
Fk = F('x0', xk, 'p', uk);
% Add contribution to objective function
J = J + Fk.qf;
% Update x
xk = Fk.xf;
x_plot{end+1} = xk;
end
% Enforce terminal conditions
g{end+1} = xk - data.xN;
% Concatenate variables and constraints
w = vertcat(w{:});
lbw = vertcat(lbw{:});
ubw = vertcat(ubw{:});
w0 = vertcat(w0{:});
g = vertcat(g{:});
% Formulate the NLP solver object
nlp = struct('x', w, 'g', g, 'f', J);
solver = casadi.nlpsol('solver', 'ipopt', nlp);
% Create a function that maps the NLP decision variable to the x and u trajectories
traj = casadi.Function('traj', {w}, {horzcat(x_plot{:}), horzcat(u_plot{:})},...
{'w'}, {'x', 'u'});
% Solve the NLP and extract solution
sol = solver('x0', w0, 'lbx', lbw, 'ubx', ubw, 'lbg', 0, 'ubg', 0);
[x_opt, u_opt] = traj(sol.x);
x_opt = full(x_opt);
u_opt = full(u_opt);
% Plot the solution
figure();
clf;
hold on;
grid on;
plot(tgrid, x_opt(1,:), 'r--');
plot(tgrid, x_opt(2,:), 'b-');
stairs(tgrid, [u_opt(1,:) nan], 'g-.');
xlabel('t')
legend('x1','x2','u')
|