Figure 2.1:

Dynamical regimes for the planar system dx/dt = Ax, A \in \mathbb {R}^{2 x2}.

Code for Figure 2.1

Text of the GNU GPL.

main.py

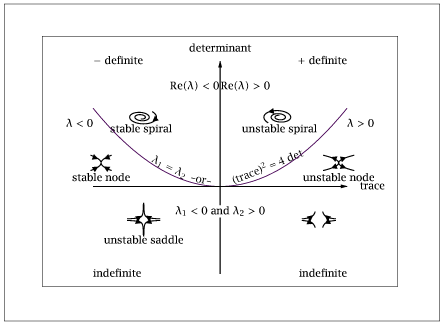
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import expm

# Axes and (trace)^2 = 4 det line
x = np.linspace(-5, 5, 101)
y = x**2 / 4
quad = np.column_stack((x, y))

lines = np.array([
    [-5, 0, 0, -7, 0, -1.5],
    [5, 0, 0, -2.5, 0, 10]
])

# Stable spiral
T = -0.2
D = (T**2 + 4) / 4
A = np.array([[0, np.sqrt(D)], [-np.sqrt(D), T]])
nts = 101
time = np.linspace(0, 15, nts)
x0 = np.array([1, 1])
xssp = np.zeros((nts, 2))
for i in range(len(time)):
    xssp[i] = expm(A * time[i]) @ x0

# Unstable spiral (reverse time)
x0 = np.array([-1, -1])
xusp = np.zeros((nts, 2))
for i in range(len(time)):
    xusp[i] = expm(A * time[i]) @ x0
xusp = xusp[::-1]

# Stable node
A = np.array([[-0.5, 0], [0, -0.25]])
x0 = np.array([1, 1])
x = np.zeros((nts, 2))
for i in range(len(time)):
    x[i] = expm(A * time[i]) @ x0
x1, x2 = x[:, 0], x[:, 1]
xsno = np.column_stack((x, -x1, x2, -x1, -x2, x1, -x2))

# Unstable saddle, trace < 0
A = np.array([[-0.3, 0], [0, 0.2]])
x0 = np.array([-1, 0.1])
x = np.zeros((nts, 2))
for i in range(len(time)):
    x[i] = expm(A * time[i]) @ x0
x1, x2 = x[:, 0], x[:, 1]
xusa = np.column_stack((x, -x1, x2, -x1, -x2, x1, -x2))

# Another unstable saddle, trace > 0
A = np.array([[-0.1, 0], [0, 0.15]])
x0 = np.array([-1, 0.1])
x = np.zeros((nts, 2))
for i in range(len(time)):
    x[i] = expm(A * time[i]) @ x0
x1, x2 = x[:, 0], x[:, 1]
xusat = np.column_stack((x, -x1, x2, -x1, -x2, x1, -x2))

# Plotting
plt.figure(figsize=(12, 10))
plt.plot(quad[:, 0], quad[:, 1], 'k-')
plt.plot(lines[:, 0], lines[:, 1], 'k-')
plt.plot(lines[:, 2], lines[:, 3], 'k-')
plt.plot(lines[:, 4], lines[:, 5], 'k-')

plt.plot(xssp[:, 0], xssp[:, 1], 'r-', label='Stable Spiral')
plt.plot(xusp[:, 0], xusp[:, 1], 'b-', label='Unstable Spiral')

for i in range(0, xsno.shape[1], 2):
    plt.plot(xsno[:, i], xsno[:, i+1], 'g-')
plt.plot([], [], 'g-', label='Stable Node')

for i in range(0, xusa.shape[1], 2):
    plt.plot(xusa[:, i], xusa[:, i+1], 'm-')
plt.plot([], [], 'm-', label='Unstable Saddle (trace < 0)')

for i in range(0, xusat.shape[1], 2):
    plt.plot(xusat[:, i], xusat[:, i+1], 'c-')
plt.plot([], [], 'c-', label='Unstable Saddle (trace > 0)')

plt.title('Complicated Planar Dynamics')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.show(block=False)

# Save data to .dat file
with open('jimphase.dat', 'w') as f:
    np.savetxt(f, quad, fmt='%f', header="quad")
    f.write("\n\n")
    np.savetxt(f, lines, fmt='%f', header="lines")
    f.write("\n\n")
    np.savetxt(f, xssp, fmt='%f', header="xssp")
    f.write("\n\n")
    np.savetxt(f, xusp, fmt='%f', header="xusp")
    f.write("\n\n")
    np.savetxt(f, xsno, fmt='%f', header="xsno")
    f.write("\n\n")
    np.savetxt(f, xusa, fmt='%f', header="xusa")
    f.write("\n\n")
    np.savetxt(f, xusat, fmt='%f', header="xusat")