Figure 2.26:

Stability regions for Adams-Bashforth methods; \dot {x}=\lambda x.

Code for Figure 2.26

Text of the GNU GPL.

main.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
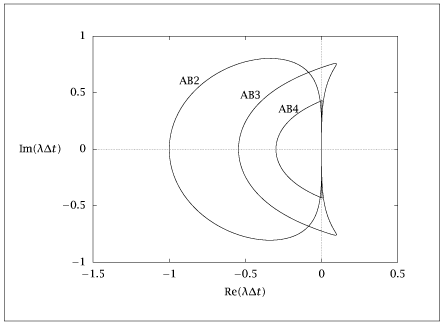
import numpy as np
import matplotlib.pyplot as plt

# Setting grid points
axisbox = [-1.5, 1.5, -1, 1]
xa, xb, ya, yb = axisbox
npts = 50
theta = np.linspace(0, 2*np.pi, 2*npts+1)
z = np.exp(1j*theta)

# 2nd order Adam Bashforth
nu2 = (z**2 - z) / ((3*z - 1)/2)

# 3rd order Adam Bashforth
nu3 = (z**3 - z**2) / ((5-16*z + 23*z**2)/12)

# 4th order Adam Bashforth
nu4 = (z**4 - z**3) / ((55*z**3 - 59*z**2 + 37*z - 9)/24)

# chop off intersecting loops for 4th order AB
for k in range(len(nu4) - 1):
    zz = np.array([np.real(nu4), np.imag(nu4)])
    iloop = 0
    for j in range(k+2, len(nu4)-1):
        # find first place where zz(k) intersects the rest of the path
        A = np.column_stack([zz[:,k]-zz[:,k+1], zz[:,j+1]-zz[:,j]])
        if np.linalg.det(A) != 0:
            lam = np.linalg.solve(A, zz[:,j+1]-zz[:,k+1])
            if np.all((0 <= lam)  & (lam <= 1)):
                iloop = list(range(k+1, j+1))
                zzint = lam[0]*zz[:,k] + (1-lam[0])*zz[:,k+1]
                break
    if iloop:
        # chop out nu4(iloop) and replace with single interpolated value zzint
        zzcp = complex(zzint[0], zzint[1])
        nu4[iloop[0]] = zzcp
        nu4 = np.delete(nu4, iloop[1:])


# Prepare data for saving
nus = np.column_stack((np.real(nu2), np.imag(nu2), np.real(nu3), np.imag(nu3)))
nus4 = np.column_stack((np.real(nu4), np.imag(nu4)))

plt.figure()
plt.plot(nus[:,0], nus[:,1], 'r')
plt.plot(nus[:,2], nus[:,3], 'b')
plt.plot(nus4[:,0], nus4[:,1], 'g')
plt.show(block=False)


# Save to AB_stability.dat file
with open("AB_stability.dat", "w") as f:
    np.savetxt(f, nus, fmt='%.17e', header="nu2 and nu3 real and imag")
    f.write("\n\n")
    np.savetxt(f, nus4, fmt='%.17e', header="nu4 real and imag")