Figure 2.28:

Stability regions for Runge-Kutta methods; \dot {x}=\lambda x.

Code for Figure 2.28

Text of the GNU GPL.

main.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
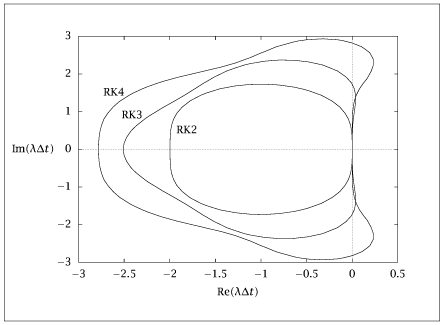
import numpy as np
import matplotlib.pyplot as plt

# Setting up the grid points
axisbox = [-4, 4, -4, 4]
xa, xb, ya, yb = axisbox
nptsx = 51
nptsy = 51
x = np.linspace(xa, xb, nptsx)
y = np.linspace(ya, yb, nptsy)
X, Y = np.meshgrid(x, y)
Z = X + 1j * Y

# Define the Runge-Kutta methods
def RK2(z):
    return 1 + z + 1/2 * z**2

def RK3(z):
    return 1 + z + 1/2 * z**2 + 1/6 * z**3

def RK4(z):
    return 1 + z + 1/2 * z**2 + 1/6 * z**3 + 1/24 * z**4

# Evaluate R(z) inside axisbox
Rval2 = RK2(Z)
Rval3 = RK3(Z)
Rval4 = RK4(Z)

# Evaluate |R(z)| for finding the region of absolute stability
Rabs2 = np.abs(Rval2)
Rabs3 = np.abs(Rval3)
Rabs4 = np.abs(Rval4)

# Generate contours
cs2 = plt.contour(x, y, Rabs2.T, [1])
cs3 = plt.contour(x, y, Rabs3.T, [1])
cs4 = plt.contour(x, y, Rabs4.T, [1])
plt.close()

def get_contour_data(cs):
    paths = cs.collections[0].get_paths()
    v = paths[0].vertices
    return v

c2 = get_contour_data(cs2)
c3 = get_contour_data(cs3)
c4 = get_contour_data(cs4)
# swap columns (not sure why this is needed: jbr)
c2[:, [0,1]] = c2[:, [1,0]]
c3[:, [0,1]] = c3[:, [1,0]]
c4[:, [0,1]] = c4[:, [1,0]]

plt.figure()
plt.plot(c2[:,0], c2[:,1])
plt.plot(c3[:,0], c3[:,1])
plt.plot(c4[:,0], c4[:,1])
plt.show(block=False)

# Save to RK_stability.dat file
with open('RK_stability.dat', 'w') as f:
    np.savetxt(f, c2, fmt='%.8f', header="c2")
    f.write('\n\n')
    np.savetxt(f, c3, fmt='%.8f', header="c3")
    f.write('\n\n')
    np.savetxt(f, c4, fmt='%.8f', header="c4")