Figure 2.30:

Approximate solutions to \eqref {eq:MWRexample} using the finite element method with hat functions for N=6 and N=12. The exact solution also is shown.

Code for Figure 2.30

Text of the GNU GPL.

main.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import solve

# Finite element solution setup
N = 5
h = 1 / (N + 1)
A = np.zeros((N, N))
u = np.zeros(N)
x1 = np.linspace(0, 1, N + 2)
b = np.zeros(N)
A[0, 0] = 2 / 3 * h - 2 / h
A[1, 0] = h / 6 + 1 / h
A[N - 1, N - 1] = 2 / 3 * h - 2 / h
A[N - 2, N - 1] = h / 6 + 1 / h
for i in range(1, N - 1):
    A[i, i] = 2 / 3 * h - 2 / h
    A[i - 1, i] = h / 6 + 1 / h
    A[i + 1, i] = h / 6 + 1 / h
b = - (np.arange(N)+1)*h**2
u = solve(A, b)
us1 = np.zeros(N + 2)
us1[1:-1] = u

# Exact solution
Nex = 100
hex = 1 / (Nex + 1)
xex = np.linspace(0, 1, Nex + 2)
uex = -xex + np.sin(xex) / np.sin(1)

# Finite element solution with larger N
N = 11
h = 1 / (N + 1)
A = np.zeros((N, N))
u = np.zeros(N)
x2 = np.linspace(0, 1, N + 2)
b = np.zeros(N)
A[0, 0] = 2 / 3 * h - 2 / h
A[1, 0] = h / 6 + 1 / h
A[N - 1, N - 1] = 2 / 3 * h - 2 / h
A[N - 2, N - 1] = h / 6 + 1 / h
for i in range(1, N - 1):
    A[i, i] = 2 / 3 * h - 2 / h
    A[i - 1, i] = h / 6 + 1 / h
    A[i + 1, i] = h / 6 + 1 / h
b = - (np.arange(N)+1)*h**2
u = solve(A, b)
us2 = np.zeros(N + 2)
us2[1:-1] = u

# Plotting
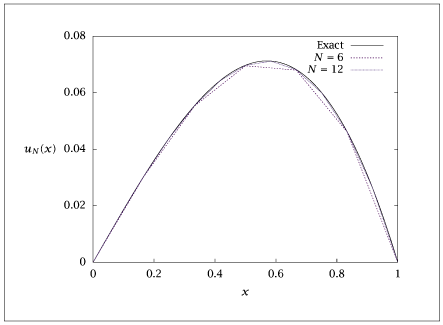
plt.plot(xex, uex, '-', x1, us1, '-.', x2, us2, '--')
plt.legend(['Exact', 'N=6', 'N=12'])
plt.show(block=False)

# Save data
t1 = np.column_stack((xex, uex))
t2 = np.column_stack((x1, us1))
t3 = np.column_stack((x2, us2))

with open("FEGalerkin1.dat", "w") as f:
    np.savetxt(f, t1, fmt='%f', header="Exact Solution")
    f.write("\n\n")
    np.savetxt(f, t2, fmt='%f', header="Finite Element N=6")
    f.write("\n\n")
    np.savetxt(f, t3, fmt='%f', header="Finite Element N=12")