Figure 3.12:

Concentration versus membrane penetration distance for different reaction rate constants.

Code for Figure 3.12

Text of the GNU GPL.

main.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
import matplotlib.pyplot as plt

nzs = 100
z = np.linspace(0, 1, nzs)
kvec = np.array([0, 2, 10, 30, 100])
cs = np.zeros((len(z), len(kvec)))

for i in range(len(kvec)):
    k = kvec[i]
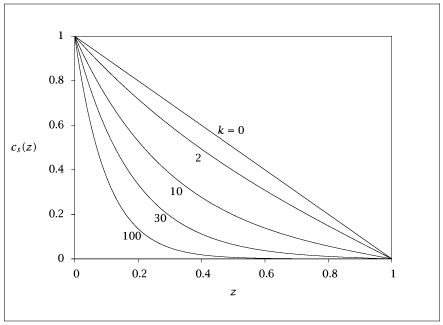
    if k == 0:
        cs[:, i] = 1 - z
    else:
        cs[:, i] = np.sinh(np.sqrt(k) * (1 - z)) / np.sinh(np.sqrt(k))

plt.figure()
plt.plot(z, cs)

nk = 3
k = kvec[nk]
tvec = np.array([0, 0.001, 0.005, 0.01, 0.05, 0.1, 1.0])
nts = len(tvec)
nterms = 25
c = np.zeros((nzs, nts))
for j in range(nts):
    t = tvec[j]
    sum_ = np.zeros(nzs)
    for n in range(1, nterms+1):
        n2p2 = n**2 * np.pi**2 + k
        term = (-1)**n * (n / n2p2) * np.sin(n * np.pi * (1 - z)) * np.exp(-n2p2 * t)
        sum_ += term
    c[:, j] = cs[:, nk] + sum_ * 2 * np.pi

plt.figure()
plt.plot(z, c)
plt.show(block=False)

# store data
store = np.column_stack((z, cs))
with open("csz.dat", "w") as f:
    np.savetxt(f, store, fmt='%f', header='store')