Figure 5.2:

Sampling faster on the last plot in Figure \ref {fig:wiener}; the sample time is decreased to \Delta t = 10^{-9} and the roughness is restored on this time scale.

Code for Figure 5.2

Text of the GNU GPL.

wiener_6.dat

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
# Time  W6
0.499995 1316.673529
0.499996 1318.096638
0.499997 1318.671473
0.499998 1318.190774
0.499999 1317.581155
0.500000 1316.602201
0.500001 1318.088506
0.500002 1317.615753
0.500003 1319.033094
0.500004 1319.918087
0.500005 1319.961433

main.py

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
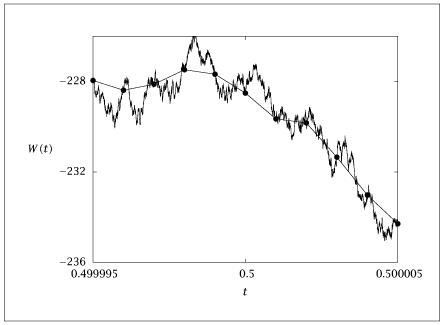
# [depends] wiener_6.dat

# This py-file loads data file 'wiener_6.dat'.
import numpy as np
import matplotlib.pyplot as plt

# restore the roughness to the finest time scale produced in wiener.m

# Load data
data = np.loadtxt('wiener_6.dat')
tdat = data[:, 0]
wdat = data[:, 1]
ndat = len(tdat)

# Parameters
nsam = 1000
del_ = 1 / nsam
npts = (ndat - 1) * nsam
D = 1

# Set seed for reproducibility
np.random.seed(0)

# Generate unit variance random variables
# then adjust the mean so the cumsum equals
# the difference in consecutive wdat values

raw2 = np.sqrt(2 * D * del_) * np.random.randn(nsam - 1, ndat - 1)
wmean = np.diff(wdat)
shiftmean = np.mean(raw2, axis=0) - wmean / (nsam - 1)
shift2 = raw2 - np.kron(np.ones((nsam - 1, 1)), shiftmean)
shiftnoise = np.vstack((np.zeros(ndat - 1), shift2))
wmat = np.kron(np.ones((nsam, 1)), wdat[:-1]) + np.cumsum(shiftnoise, axis=0)
w = wmat.ravel(order='F')
deltat = np.kron(np.diff(tdat), np.linspace(0, 1, nsam, endpoint=False))
tmat = np.kron(tdat[:-1], np.ones(nsam)) + deltat
time = tmat.ravel()

# The generated sequence (time, w) should pass through the data
# (tdat,wdat) but display the Wiener process roughness between the data
# points

plt.plot(tdat, wdat, '-o', label='Original Data')
plt.plot(time, w, label='Wiener Process')
plt.legend()
plt.show(block=False)

# Combine fine and rough data into a single file and arrange as matrices for np.savetxt
original_data = np.column_stack((tdat, wdat))
combined_data = np.column_stack((time, w))

with open('wexpand.dat', 'w') as f:
    np.savetxt(f, original_data, fmt='%.15f', delimiter='\t', header="[rough]")
    f.write("\n\n")
    np.savetxt(f, combined_data, fmt='%.15f', delimiter='\t', header="[fine]")