Polyelectrolyte Complexation
Debbie Audus
CHE210D Spring 2009 Final Project
Summary
Two oppositely charged polymers are studied using molecular dynamics. At high enough electrostatic strengths, these polymer form complexes. The radius of gyration squared of these complexes is calculated as a function of polymer length (N) and electrostatic strength (λ). The resulting trends are the effect of various interacting driving forces.
Background
When two oppositely charged polymers are combined in solution, they can form a complex. The structure and properties of this complex will depend on a wide variety of parameters including the length of the polymers, the concentration, the strength of the electrostatics and the chemical composition of the polymers. Here, we study the effect of the lengths of the polymers and the strength of the electrostatics on the radius of gyration squared. Complexes such as those described in this study can be used for a variety of applications such as drug delivery since the complexes can encapsulate other molecules (Thünemann et al. 2004).
Simulation methods
To accurately represent the polymers, three pair potentials
are required. The first is a harmonic bond stretching term between monomers (
). The second is a purely repulsive
Lennard-Jones potential term between non-bonded monomers (
for 
). The third term is an electrostatic
term that is a screened Coloumb potential (
) where γ is 1 for monomers of the
same charge and -1 for monomers of opposite charge. λ is a measure of the
electrostatic strength, which is varied in this study. κ is the screening
length which has been set so that the electrostatic interaction between two
monomers is 1e-4 at one third of the box length. With this convention, the
screening effect at short ranges is very small. The box length is determined
such that the non-dimensionalized polymer concentration is fixed at 2.2e-7N.
Since the length of the polymers (N) ranges from 10 to 80, a molecular dynamics simulation is used for efficiency. Since we would like to investigate the system at a specified temperature, an Andersen thermostat is used to maintain the non-dimensionalized temperature of 1.2. This particular implementation uses single particle collisions. The error associated with radius of gyration is computed using a block averaging scheme as described in Allen and Tildesley (1994).
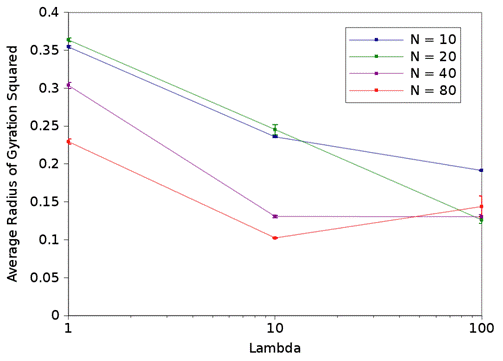
Figure 1: Squared radius of gyration as a function of the electrostatic strength (λ) for a variety of polymer lengths (N).
Figure 2: Snapshots of equilibrated structures for N=80 and λ=10 (left), 100 (right).
Results and interpretation
The results shown in figure 1 are quite interesting since there is not a single general trend that applies to all of the results. However, these results can be understood by looking at the driving forces. The contribution due to the electrostatic parameter, λ, is complex since oppositely charged monomers attract and same charged monomers repulse. At lower values of λ, the attraction dominates and increases with λ. However, at large values of λ, the monomer repulsion is so strong, it forces a rod-like conformation as seen in figure 2. For longer polymers, this creates a larger radius of gyration squared. Therefore, a minimum in the radius of gyration occurs between λ=1 and λ=100 for N=40 and N=80. The effect of N is also complex since an increase in N in the absence of electrostatics increases the radius of gyration due to the repulsive nature of the monomers. Conversely, increasing N increases the polymer charge, which reduces the radius of gyration squared. Based on figure 1, we can conclude that increase in charge dominates for the N=40 and N=80 cases, and that there is a crossover between the dominating force for N=10 and N=20.
Two major improvements may be made to the model. The first is the use of either an explicit solvent or Brownian dynamics as done by Winkler et al. (2002) to more accurately model the implicit solvent. The second is to use unscreened electrostatics using the Ewald sum technique. This model could also be studied more in depth by looking at other parameters such as concentration.
Movie
The movie shows two oppositely charged polymers with N=80 and λ= 10 as a function of simulation time. A spiral structure can be seen in the polymer complex.
Source code
References
R. G. Winkler, M. O. Steinhauser, and P. Reineker. Physical Review E, 66:021802, 2002.
M. P. Allen and D. J. Tildesley. Computer Simulations of Liquids. Clarendon Press, 1994.
A. F. Thünemann, M. Müller, H. Dautzenberg, J.F. Joanny, and H. Löwen. Advances in Polymer Science, 166:113, 2004.