The Hydrophobic Interaction in a Spherically-Symmetric Water Bath
Aviel Chaimovich
CHE210D Spring 2009 Final Project
Summary
The hydrophobic interaction (HI) is perhaps the most significant driving-force in living organisms. In this work, I demonstrate a fundamental particularity of the HI: the notion that it is mostly caused by the medium. I employ a Monte Carlo simulation to achieve this task.
Background
The HI essentially describes the association of non-polar molecules in a water medium. Ironically, while these molecules are nearly inert in vacuum, they virtually bond in water. Thus, it is believed that water’s presence is mainly responsible for the HI.
Simulation methods
A spherically-symmetric model
for water is used, one which was optimized via the relative entropy multiscale
procedure [1]. A
conventional (methane) model is used for the hydrophobes. The solvent
interacts with the solutes via Lorentz-Berthelot mixing rules. The simulation constructs
a (periodic) box with 216 freely-moving water molecules. A certain number of
hydrophobic molecules, 
, is constrained at the center, and a single
hydrophobic molecule is allowed to traverse along a single axis (the reaction
coordinate of interest). This scenario is a simple representation for the water-mediated
association between a pair of non-polar molecules, having same size yet
different energetics. The corresponding potential of mean force, 
, is evaluated via an iterative flat-histogram method,
the multicanonical algorithm [2]. This is a measure of the HI; importantly, it is a linear
combination of the direct interactions between the pair (the potential energy) and
the indirect interactions of the medium (the free energy).
Results and interpretation
The simulation-determined 
exhibits oscillatory behavior, comparable in
energetics with works utilizing more realistic models for water [3,4]. With
increasing (relative
strength of the stationary hydrophobe), the energetics of become only modestly more pronounced. While the
energetics of the free-space interaction scale linearly with , the energetics of scale much more weakly with . This stems in the fact that the potential energy
between the hydrophobic molecules has little contribution in the HI. Along the
same lines, the effect of the water medium on the HI becomes even more dominant
as the hydrophobic pair is separated away (considering that the inner well scales with 
and the outer well scales with 
). This is simply explained by the fact that
hydrophobes barely feel each other beyond their van der Waals radius. Nevertheless,
there is much uncertainty in . Its statistics can be greatly enhanced by invoking
a more sophisticated flat-histogram method (i.e., the transition-matrix
algorithm). For subsequent work, it will be also interesting to examine more
realistic many-body configurations (e.g., two stationary molecules constructed as
a “dumbbell” rather than overlapping each other).
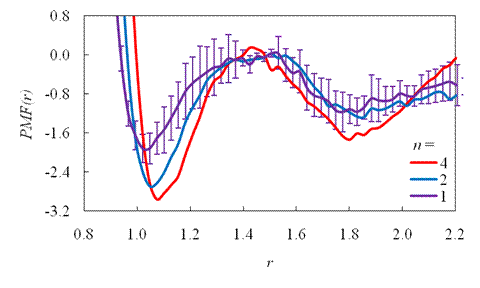
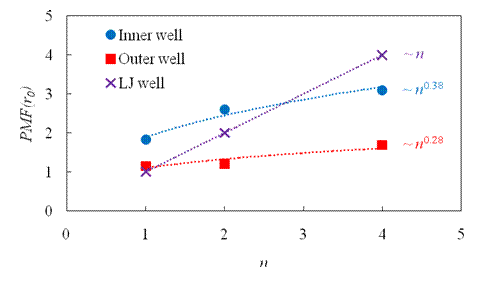
Figure: the dependence
of 
on 
. The
top graph presents in terms of separation distance for several . Each curve is shifted so that the energetic value
of its barrier is zero. For clarity, error bars are only given for 
(all other have comparable errors). Notice that as doubles, both wells only slightly deepen. The bottom
graph presents both wells in terms of . The scaling law for each trend is shown. For
comparison, the free-space (Lennard-Jones) well is also given. Notice that the
slope for the free-space well is substantially steeper than for the two wells.
Movie
The movie depicts the
hydrophobic interaction. It is the zero iteration (the unperturbed canonical
ensemble) for (the hydrophobes are energetically equivalent). The
water molecules are gray, while the hydrophobic molecules are yellow. For
transparency, the size of the water molecules is scaled down. Notice that the
moving hydrophobic molecule samples its reaction coordinate via curve above.
Source code
References
1. Chaimovich, A. and M.S. Shell, Anomalous waterlike behavior in spherically-symmetric water models optimized with the relative entropy. Physical Chemistry Chemical Physics, 2009. 11(12): p. 1901-1915.
2. Berg, B.A. and T. Neuhaus, Multicanonical ensemble: A new approach to simulate first-order phase transitions. Physical Review Letters, 1992. 68(1): p. 9.
3. Moghaddam, M.S., S. Shimizu, and H.S. Chan, Temperature Dependence of Three-Body Hydrophobic Interactions: Potential of Mean Force, Enthalpy, Entropy, Heat Capacity, and Nonadditivity. Journal of the American Chemical Society, 2005. 127(1): p. 303-316.
4. Czaplewski, C., et al., Molecular Origin of Anticooperativity in Hydrophobic Association. The Journal of Physical Chemistry B, 2005. 109(16): p. 8108-8119.