The Radius of Gyration for Charged Polymers
Peter Chung
CHE210D Spring 2009 Final Project
Summary
In random coil behavior, there is a power-law relationship between the radius of gyration and the polymer length:
Rg = R0 Nν
Theoretically and experimentally, it has been shown that for uncharged polymers ν » ½. Recent experimental evidence has shown that the radius of gyration for charged chemically unfolded proteins has a power-law exponent of ν = .605 ± .0271. A Monte-Carlo simulation of a linear polymer with a Lennard-Jones and screened Coulomb potential was done to confirm the experimental results.
Background
The problem of protein folding is generally complicated by the fact that it usually does not start from a single reference state; even in the presence of denaturing agents, a protein might exhibit a secondary structure that limits the kinetic pathways for folding of the protein2. The aim of understanding the radius of gyration for charged polymers is to elucidate upon this ensemble of partially folded states which do not follow random coil behavior.
Simulation methods
The model that will be used in this simulation is a combination of the Lennard-Jones potential and screened Coulomb potential. The primary contribution of the Lennard-Jones potential was to provide the excluded volume so that the subunits do not stick. The screened Coulomb potential was used, as each subunit is charged and there exists a Debye screening length of 10 angstroms, per experimental conditions. As such, the resulting potential in reduced units took the following form:
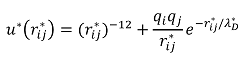
The Monte-Carlo algorithm was used in order to determine the radius of gyration with the aforementioned potential. As in the experiment, it was assumed that the ensemble average radius of gyration had reached thermal equilibrium. Due to limitations in computing power, polymers simulated were much shorter; to account for various charge distributions, simulations with a uniform charge distribution, a randomly positively charged distribution, and a randomly positively and negatively charged distribution were performed in the hopes that it would still accurately capture the power law behavior borne out by experiments.
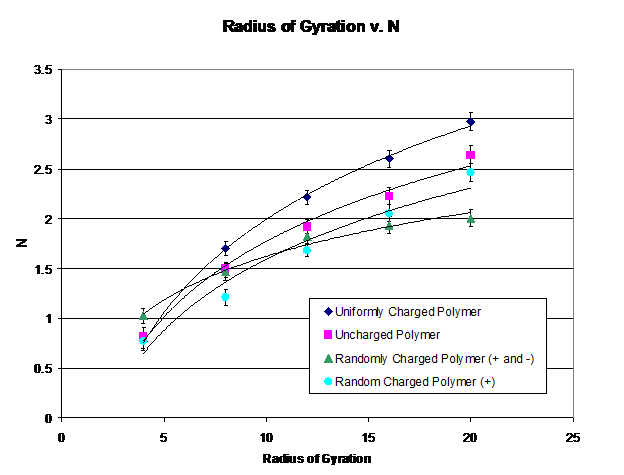
Figure 1: The Monte Carlo simulation results for the radius of gyration under different charged polymer conditions. Note that each follows a power law behavior.
|
Type of Polymer |
α (νcharged / νunchaged) |
|
Uniformly Charged Polymer |
1.235 ± .086 |
|
Randomly Charged Polymer (+ and -) |
.5782 ± .132 |
|
Randomly Charged Polymer (+) |
.9421 ± .097 |
Table 1: The ratio of the power law exponents for the charged and uncharged polymers obtained from Monte-Carlo radius of gyration simulations.
Results and interpretation
A Monte-Carlo simulation was run for N = 4, 8, 12, 16, 20 subunits in uniformly charged, uncharged, randomly positively and negatively charged, and randomly positively charged conditions. To minimize error, 400,000 moves were taken per particle and five simulations were done for each result. The α ratio values for the uniformly charged polymer on Table 1 (αsimulation = 1.235 ± .086) correspond quite nicely to the α found in the experimental papers (αexperimental = 1.21 ± .054), however, the randomly positively and negatively charged and randomly positively charged polymers do not quite fit with prior experimental observations. However, it is gratifying to see that even with charged polymers the expected power law behavior was observed.
For the randomly positively and negatively charged polymer, this is to be somewhat expected: attractive forces should lower the radius of gyration. However, to the extent that it did for the simulation was rather surprising.
Due to the limitations of computing power, the polymers in the simulations could not be very long, as opposed to denatured proteins which have an order of magnitude more subunits. While the expectation was that randomly distributed non-integer charges on each subunit would be sufficient in order to simulate a polymer much larger, according to Figure 1 that was clearly not the case. The model might be improved by including only integer charges (as that gave the closest α to the experimental result) and running the simulation for more subunits. Furthermore, it might be helpful to obtain and simulate actual Protein sequences to compare the experimental values of each protein with their corresponding simulation values.
Movies
The movie depicts a randomly positively and negatively charged polymer evolving over 400,000 steps per particle. Note the presence of repulsive and attractive Coulombic forces, causing parts of the polymer to seemingly aggregate.
Source code
References
- Jonathan Kohn et. al. 2004. Random-Coil Behavior and the Dimensions of Chemically Unfolded Proteins. PNAS 101(34): 12491-12496.
- Shortle, D. 1996. The denatured state (the other half of the folding equation) and its role in protein stability. FASEB J. 10: 27–34.