Scaling law in thickness of polymeric brushes
Su-Mi Hur
CHE210D Spring 2009 Final Project
Summary
Here I study how polymer brush layer thickness changes depending on the polymer chain length N and grafting density ρ is studied through MD simulation. Each polymer chain is modeled as beads and springs with shifted LJ and harmonic potentials. An additional harmonic potential between grafting point and first bead in the chain, as well as, a wall potential that interacts with all monomers is introduced. Obtained results shows that high of brush layer h increases linearly as N increases. h does not depend on ρ for small values of ρ . However, h increases as ρ increases for higher values of ρ and observed scaling follows theoretical prediction.
Background
One important class of polymeric systems are brush systems, where the end of the polymer chain is tethered to a surface. These systems are related colloidal stabilization, lubrication, surface modification, etc. When multiple chains are tethered, a “grafting layer” or “polymeric brushes” are formed, and the thickness of the layer scales differently than polymer that are non-tethered . There have been theoretical predictions and studies with simulations and experiment. A simple scaling argument using a Gaussian chain model with the Flory approximation predicts (Alexander 1977) h ~ N ρ1/3, when a uniform monomer density up to height h from the grafting surface is assumed. Even though density of monomer is not uniform, this simple scaling of h is has been confirmed in several simulations. In this study, the scaling of h is tested using a simple model. Scaling and monomer distribution changes are studied by varying grafting density ρ and polymer length N.
Simulation methods
Each polymer chain is modeled with beads and springs. Similar to the homework 3, non-bonded polymer monomers interact with Lennard-Jones potential which is cut and shifted at rc=2.5, while bonded monomerss interact with a harmonic potential (k=1000, r0=1). In order to model the tethered chain, first particle in each chain has additional harmonic potential k/2 (r1, i - r0, i)2 , where r0, i is a grafting points of ith chain which are generated randomly on the surface. There is also repulsive wall potential, 4(z/10)-12, which prevents polymer chains from crossing the grafting surface.
NVE molecular dynamics simulations are conducted with the velocity Verlet integration. The simulation box is periodic in x and y directions, while the box size in z direction is semi-infinite (z>0). Box size in x and y directions are fixed at L=10, and number of polymer chains is determined by grafting density ρ (number of polymer chain / L2 ). However, for very small values of ρ (0.001), a larger box size is used to satisfy grafting density constraint. Initially, each polymer chain is stretched vertically from the grafting point and each bond is stretched to 1.5 r0 (every monomer in a same polymer chain has the same x and y coordinates, while z value varies), with slight offset. The Conjugate Gradient method is used to find minimum energy configuration prior to MD. Then, an equilibration period is run with velocity rescaling. A second equilibration period is run to set the instantaneous energy the same as the target energy. For the production run, an average polymer density as a function of z is obtained.
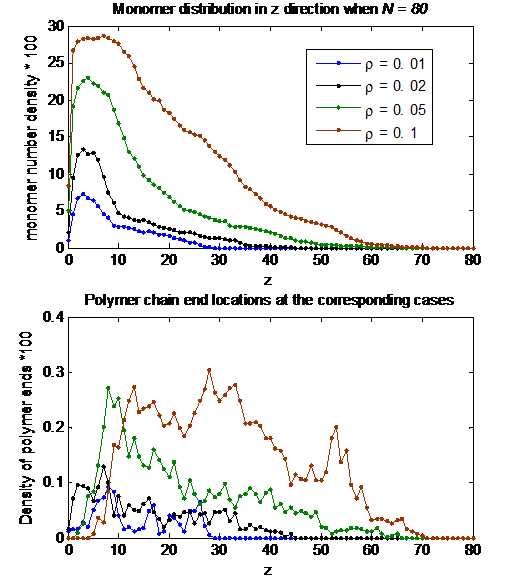
Figure 1. Monomer distribution along z-direction under various ρ at fixed N=80 (top); location of polymer chain ends for the corresponding cases (bottom).
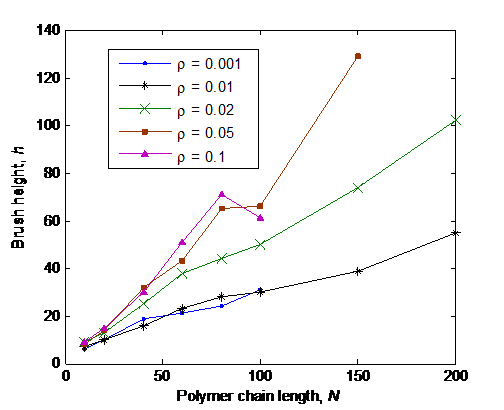
Figure 2. Brush height h as a function of N for various ρ .
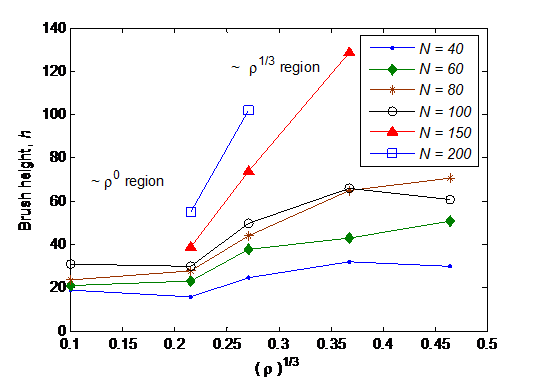
Figure 3. Brush height h as a function of ρ for various N.
Results and interpretation
Figure 1 shows how monomer density changes along z direction, when polymer chains are tethered at z = 0. It shows mushroom-like distribution of monomer along z, rather than uniform in z direction. The polymer end distribution in the bottom of Figure 1 shows that locations of the non-tethered polymer end are found over the entire z domain except close to the surface, z=0, rather than only at the boundary of the brush layer (around z = h). Figure 1 show brush layer thickness increase as ρ increases. However the general form of the profile does not change much for the simulated ρ values.
In the figure 2, brush height h is plotted as a function of polymer chain length. In this figure we can confirm that h is related to N linearly (h ~ N), within expected error. The difference between ρ =0.001 and ρ=0.01 is small since at low ρ, polymer chains do not interact with neighboring chains. However, above ρ = 0.01, brush layer gets thicker as ρ increases. The detailed relation between h and ρ is shown in the Figure 3, which is plot of h as a function of ρ1/3. We can see that after ρ independent region, h scales as ρ1/3. The slope increases as N increases (h ~ N). Thus, we could confirm the simple scaling law h ~ N ρ1/3. Data for higher ρ has smaller error since more chains are simulated within a fixed box size. In order to reduce the error for smaller grafting densities, I ran 5 trials and computed the average. However, the error is large for the smaller ρ. The error could be reduced by running more trials or using a larger simulation box.
Due to time constraints, only limited data could be collected. I expect that more data would help to confirm linear relation between h and ρ1/3. At very high grafting densities, where polymer chains may be highly stretched, we may need to replace the harmonic potential for the bonds to another potential function that diverges at physical limit of chain stretching. In order to model polymer in a good solvent more accurately, we could use a LJ potential shifted at the minima, which does not have attractive well.
Movies
1. [movie1] Tethered polymers with various polymerization index N (10, 20, 40, 100, 200 and 300, sequentially) at a same grafting density ρ = 0.01. Periodic boundary conditions are imposed in x and y directions with box size L=10. Two ends of polymer chains are marked as black. The height of brush layer increases as N increases.
2. [movie2] Tethered polymers with various grafting density ρ (0.001, 0.01, 0.02, 0.05, 0.1 and 0.2, sequentially) at a same polymerization index N=80. Periodic boundary conditions are imposed in x and y directions with box size L=10 except for the case ρ =0.001 (which requires a larger box, L =31.6228, to maintain the grafting density). Again, two ends of polymer chains are marked as black. The height of brush layer increases as ρ increases, while for the small ρ = 0.001 and 0.01, high of brush does not change much.
Source code
References
“Monte Carlo and Molecular Dynamics Simulations in Polymer Science” by Kurt Binder
S. Alexander, J. Physique 1977, 38, 977.