Clustering of sodium chloride in implicit water solvent
Brandon Knott
CHE210D Spring 2009 Final Project
Summary
Simulation of nucleation from solution in condensed phases at constant chemical potential can be achieved by utilizing an accurate effective potential with implicit solvent. The distribution of cluster sizes in a metastable system is an important parameter for nucleation, as this process is driven by microscopic fluctuations in density. Here I present grand canonical Monte Carlo results showing that increasing the chemical potential in a system of chloride and sodium ions shifts the cluster size distribution towards larger clusters, a trend that makes a fluctuation large enough to form a critical-sized nucleus more likely.
Background
NaCl nucleation from solution at constant chemical potential is, in general, computationally intractable in condensed phases because insertion moves are almost uniformly rejected. For this reason, many details of this process are still unknown. Valuable information that success in this area could yield includes the height and shape of the free energy barrier to nucleation and the size, shape, and structure of the critical nucleus. For example, the structure of the critical nucleus could have implications for the two-step model of nucleation.
Simulation methods
Nucleation is driven by spontaneous density (and perhaps structure) fluctuations in a metastable phase. The distribution of cluster sizes is thus an important aspect of the nucleation process. The model used here to study clustering is an effective potential for sodium chloride in implicit water solvent[1]. This model was developed to describe the thermodynamics of salt solutions accurately and includes energy contributions from Lennard-Jones interactions, a Coulombic term (corrected for the changing dielectric of the water due to the charged species), and a repulsive Gaussian term to model the solvation shell around ions. I have modified the potential with an exponential damping term (screened “Yukawa”).
I performed Monte Carlo (MC) simulations in the grand canonical ensemble with the potential described above. In addition to displacement moves, insertion and deletion of oppositely-charged ion pairs are included to allow fluctuations in particle number. Ions are inserted and deleted in pairs in order to conserve the total charge of the simulation box. Two ions are counted as part of the same cluster if their intermolecular distance is less than or equal to a distance that corresponds to a distance slightly larger than the minimum in the interaction potential between oppositely charged ions. I studied three different chemical potentials to investigate how this parameter affects the distribution of cluster sizes.
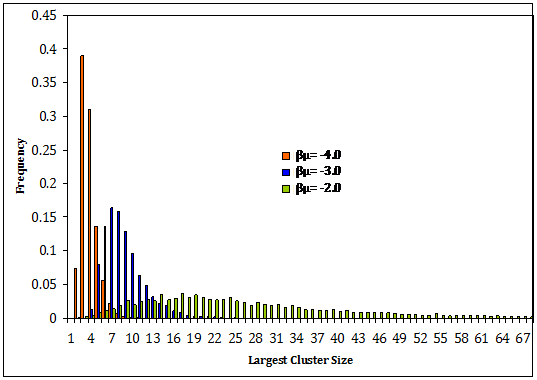
Figure 1: Histograms showing that as the chemical potential (βμ) is increased, the mean and the variance of the cluster size distribution also increases.
Results and interpretation
Figure 1 shows the effects that the chemical potential has on the distribution of the largest cluster in the system. As the chemical potential is increased, the mean of the distribution of cluster sizes is also increased, as is the variance. Increasing the chemical potential forces molecules closer together, forming larger clusters.
Nucleation is an activated process that relies on microscopic fluctuations to drive the system over a high free energy barrier. The coordinate that describes progress toward nucleation is generally taken as the size of the largest cluster in the system (although there are several different ways that a cluster can be defined). Figure 1 shows that as the chemical potential is increases, the likelihood of the appearance of a large cluster is increased. This will drive the system towards nucleation by lowering the free energy barrier to nucleation.
In the future, I will compute the free energy barrier to nucleation within this model. I will also perform free energy calculations along the nucleus size coordinate in a system with explicit solvent to compare with the implicit solvent results. I will overcome the usual problems with simulating nucleation from solution in condensed phases described in the Background section by incrementally mapping out the free energy surface by computing the microscopic driving force for nucleation (i.e. the free energy change upon adding one solute from the bulk solution to the nucleus) at each discrete cluster size from monomers to post-critical sizes.
Movie
This movie shows the “melting” of a charge-ordered cubical cluster of 125 sodium chloride atoms (only displacements are attempted in this movie; the particle number is constant). The experimentally measured size ratio of chlorine (green) to sodium (purple) atoms is about 3:1; this is reproduced in this movie. Note that the chlorine atoms diffuse away from the area of the nucleus faster than do the sodium atoms; this is due to the scaling of the maximum attempted displacement in the Monte Carlo algorithm for each type of ion to match the scaling of the diffusion coefficients of each ion (DCl : DNa ~1.5:1). Also note the Incredible Hulk coloring scheme.
Source code
References
1. Lenart, P.J., A. Jusufi, and A.Z. Panagiotopoulos, Effective potentials for 1 : 1 electrolyte solutions incorporating dielectric saturation and repulsive hydration. Journal of Chemical Physics, 2007. 126(4).