Bassam Bamieh
Welcome to my website. I am a Professor of Mechanical Engineering at the University of California at Santa Barbara (UCSB). I also have a courtesy appointment in the department of Electrical and Computer Engineering, and I am a member of the Center for Control, Dynamical Systems and Computation (CCDC). This interdisciplinary center brings together faculty and graduate students from across the College of Engineering departments and Mathematics.
My core research area is Controls and Dynamical Systems (CDS), and I do quite a bit of cross-disciplinary work at the interface between CDS and other fields such as Network Science, Fluid Mechanics, Statistical Physics, Machine Learning and Mathematics. The “Research” links to the left contain more information about the research work of my group.
New(s)
I was recently interviewed on the In-Control Podcast  | Poorva's paper on localization phenomena in large-scale networks just appeared in Control Systems Letters, and the expanded version on arXiv 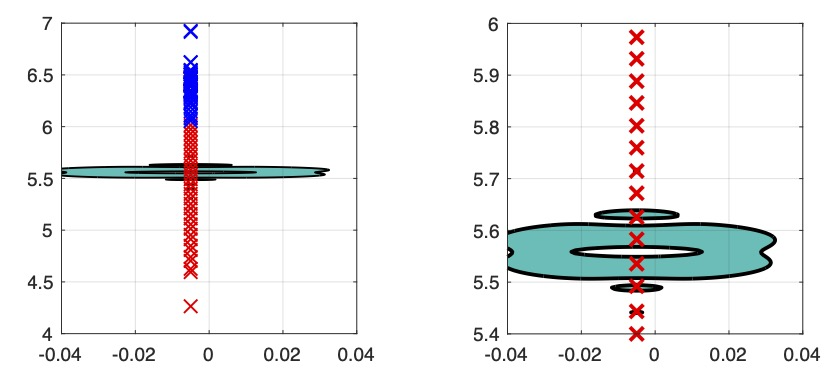 | Karthik's paper on Parametric Resonance in Networked Oscillators 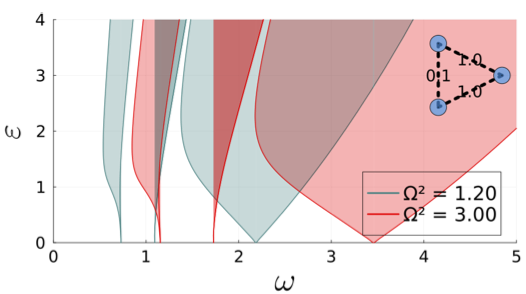 |
A new perspective on classical Linear-Quadratic optimal control problems 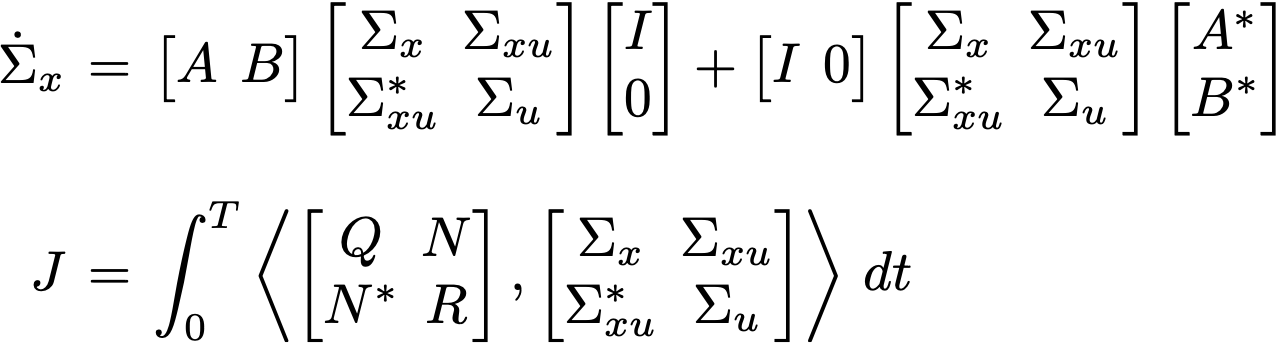 | Pascal's paper on “spurious modes” just appeared in the Journal of Computational Physics, and arXiv 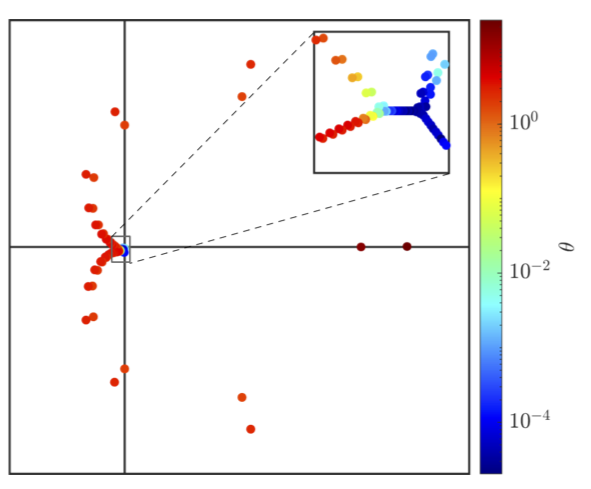 | Max's paper Continuum Swarm Tracking Control: A Geometric Perspective in Wasserstein Space won the Outstanding Student Paper Award at the 2023 CDC,his earlier paper Optimal Combined Motion and Assignments with Continuum Models won the IFAC Young Author Award at the IFAC NecSys22 conference. 
|
Lecture Notes & Tutorials
Book drafts
Lecture Notes on Linear Algebra and Functional Analysis This is a partial draft of a textbook I am writing on functional analysis and linear algebra for systems and controls research.
Lecture Notes on Vibrations A partial draft of a textbook I am writing on vibrations which I teach to 3rd year Mechanical Engineering students at UCSB.
Tutorial Papers
Discovering Transforms: A Tutorial on Circulant Matrices, Circular Convolution, and the Discrete Fourier Transform: How would you “discover” the Fourier (and other) transform if you had never heard of it? This is a different way to think about a large class of transform methods as a linear algebra (or functional analysis) problem of simultaneous diagonalization of a class of matrices or operators.
A Tutorial on Solution Properties of State Space Models of Dynamical Systems: The matrix exponential, the Peano-Baker Series, the Variations of Constants (Cauchy) formula, and the Picard iteration are various manifestations of one concept, namely the Neumann Series. All these various formulas can be “discovered” (including the definition of the matrix exponential) through various applications of the Neumann series when interpreted with a slight bit of abstraction.
A Tutorial on Matrix Perturbation Theory (using compact matrix notation): Analytic matrix perturbation theory is an immensely useful tool in many areas. It is very ironic (to me) that standard treatments of this theory do not use matrix notation! Here I present this theory using compact matrix notation which I believe simplifies the usually messy formulas and gives some additional insight. In particular, the matrix Sylvester Equation plays a prominent role in finding the eigenvectors perturbations.
A Short Introduction to the Koopman Representation of Dynamical Systems: The title describes what this is. I try to develop the basic concept with the minimum of unnecessary distractions. In particular, special attention is paid to the duality between initial conditions and output maps in both the original system and its Koopman representation (i.e. initial conditions of the original system become output operators in the Koopman representation and vice versa).
