Frederic Gibou - Teaching

Level Set Methods and their Applications

Aims

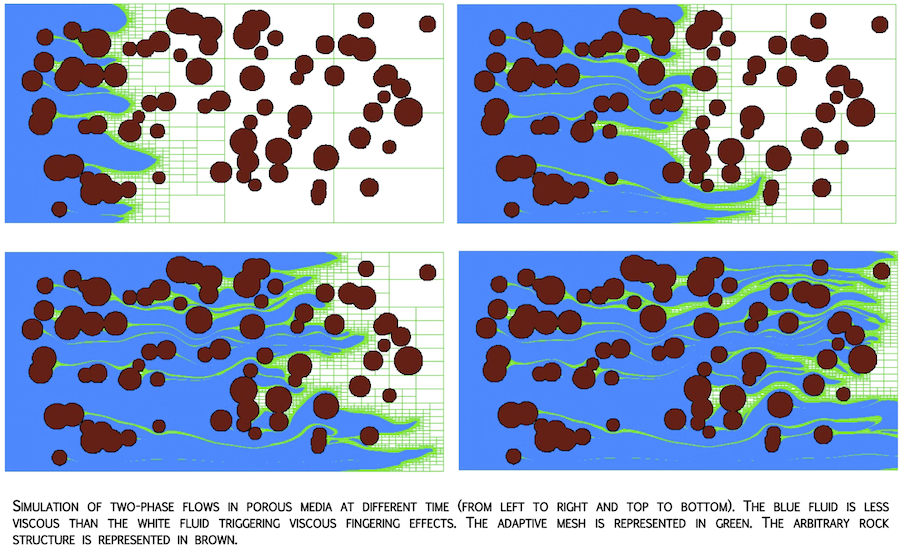
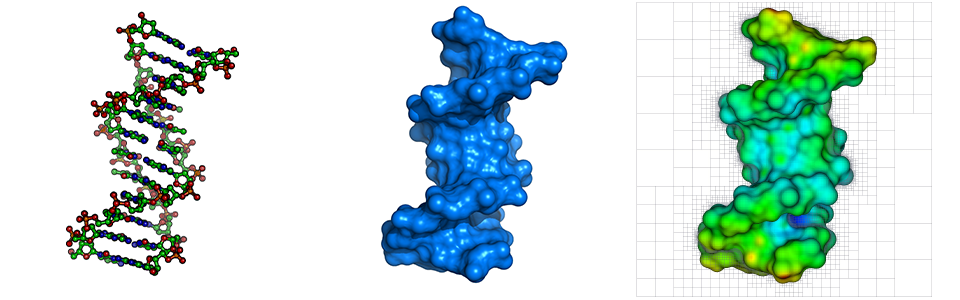
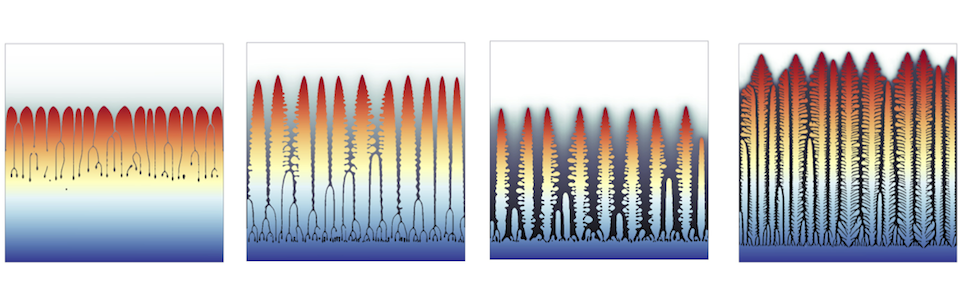
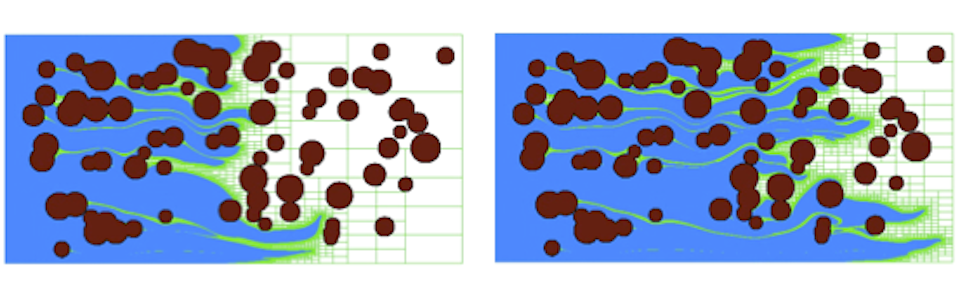
The level set method is a general technique to keep track of a moving boundary that can undergo topological changes such as the merging and the breaking of complex mutiphase flows. Since its introduction by Osher and Sethian in 1987, it has received considerable attention and applications have ranged from traditional fluid dynamics to materials science, computer vision and computer graphics. Some results obtained with this technique are given below.

The advantage of the level-set approach is that it uses an implicit representation of a moving front, hence trivializing the treatment of topological changes. On the other hand, treatment of boundary conditions on the moving front require special attention.

The goals of the first part of this course is to present the level-set representation, its equations and how they are discretized numerically, and how to impose typical boundary conditions at the moving front. The goals of the second part of the course is to expose students to an array of research topics that use the level set method. Topics will be taken from the literature or from the student's own research.

Syllabus

The syllabus for the course can be found Here.

Text Books

The optional textbook for the course is Level Set Methods and Dynamic Implicit Surfaces, by Osher and Fedkiw. Other interesting textbooks present material covered in this course:

Level Set Methods and Fast Marching Methods, J.A. Sethian.
Finite Difference Schemes and Partial Differential Equations, J. Strikwerda.
Numerical Methods for Conservation Laws, R. Leveque.
Riemann Solvers and Numerical Methods for Fluid Dynamics, E. Toro.
Numerical Analysis, R. Burden and J. Faires.
Elementary Applied Partial Differential Equations, R. Haberman.

Grading Policy

Your grade will be based on homework (50%) and a final project (50%). The goal of the project is to demonstrate the ability to use the level set method in a practical application. Examples include Free Surface Flows, Multiphase Flows, Image Segmentation, Graphics, Differential Geometry, etc. The presentations will be about 20-30 min with an additional 5-10 min for questions.