The Computational Paradigm of CASL
Our research group focuses on the design, the implementation and the application of novel computational strategies for solving problems previously untractable in science and engineering. In the large majority of applications that are described by partial differential equations, the domains of integration have irregular shapes (often moving) so that no closed-form solutions exist. Numerical methods face three main challenges: First, the description of the physical domain must be versatile enough to account for the motion of free boundaries. Second, boundary conditions must be imposed at the boundary of the irregular geometry or moving front. Finally, typical scientific applications exhibit solutions with different length scales. Examples include boundary layers around objects in the context of fluid flows, the electric double layer in the context of electrostatics or the rapid variation of solute concentration near the solidification front of metal alloys. From the numerical point of view, small length scales are related to very fine grids for which uniform grids are too inefficient to be practical. Our group's strategy is to develop computational methods on Quad-/Oc-trees grids in the level-set formalism (Quad-/Oc-trees are data structures that enable a continuous variation in the size of the computational cells). Also, since large computations in three spatial dimensions require the use of parallel architectures, our group extends the Quad-/Oc-trees strategy to the case of parallel environment. Finally, we are using Machine Learning algorithms in order to solve forward and inverse problems as well as for computing physical quantities that are challenging/impossible to obtain with standard numerical approaches.
High-Resolution Parallel Framework
The following figure is an example of the simulation of a growing crystal of a pure substance (Stefan problem - we have extended this framework to simulate binary and multialloy growth with application to Additive Manufacturing). On the left figure, a cross-section of the Octree grid is depicted in green. In particular, the grid is automatically refined near the moving front, enabling the accurate description of the important physics at this location. On the right figure, the color map represents the processors rank (blocks of the same color indicate that the parallelization [domain partitioning] is effective).


Machine Learning
We introduced a scalable strategy for development of mesh-free hybrid neuro-symbolic partial differential equation solvers based on existing mesh-based numerical discretization methods. Particularly, this strategy can be used to efficiently train neural network surrogate models for the solution func- tions and operators of partial differential equations while retaining the accuracy and convergence properties of the state-of-the-art numerical solvers. The neural bootstrapping method is based on evaluation of the finite discretization residuals of the PDE sys-tem obtained on implicit Cartesian cells centered on a set of random collocation points with respect to trainable parameters of the neural network. We applied this strategy to the important class of elliptic problems with jump conditions across irregular interfaces in three spatial dimensions. Once trained, simulations take milliseconds on laptops, providing remarkable tools for exploring large parameter spaces. The algorithms are implemented in a software package named JAX-DIPS , standing for differentiable interfacial PDE solver. JAX-DIPS is purely developed in Google JAX , offering end-to-end differentiability from mesh generation to the higher level discretization abstractions, geometric integrations, and interpolations, thus facilitating research into use of differentiable algorithms for developing hybrid PDE solvers.
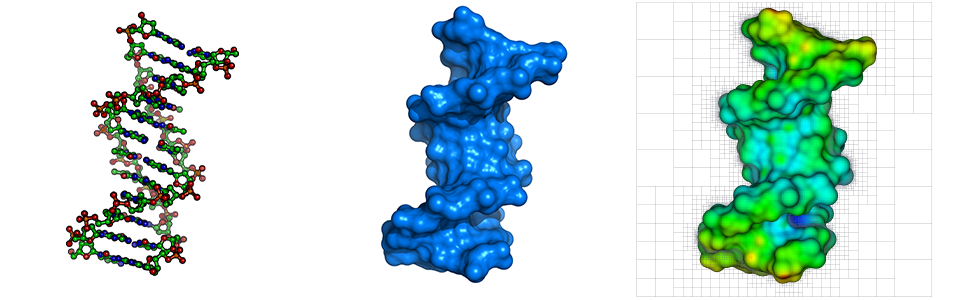
The following figure gives another example of how the use of Machine Learning can impact the computation of physical quantities (e.g. curvature ~ surface tension), especially in underresolved regions. The left figure depicts an interface with sharp features, which are difficult to approximate numerically. The case of sharp feature and underresolved regions is bound to occur during a typical simulation, especially in the important case of topological changes (merging or pinching of fronts). In addition, it is precisely in those regions that curvature plays its most important role as surface tension is largest in those regions. The figure in the center shows the results of the computation of curvature on a Octree grid using standard numerical formulaes. The right figure considers the same problem using a hybrid approach based on numerical approximations coupled with Machine Learning algorithms. Clearly, the use of Machine Learning produces highly accurate results compared to traditional approaches. This impacts countless simulations, from multiphase flows to additive manufacturing.
Computational Materials Science
Historically, new materials have been developed at a pace commensurate with the design of advanced engineering systems, providing a path for their implementation and motivating continued innovation. However, as design cycle times have shortened significantly over the past decade it has become clear that experimentally-driven materials development is no longer synchronized with that cycle. It is therefore crucial to develop and implement new computational strategies that will both accelerate discovery and reduce the period between discovery of new materials and their deployment in new technologies; it is one of the central premises of the Materials Genome Initiative (MGI). To this end, we develop and employ a suite of high performance computational strategies that will fill critical gaps in the Materials Genome infrastructure. The long-term vision is for a radically changed environment for the Materials Scientists and Engineers. Two materials themes have been selected to demonstrate the major impacts of the ongoing development of an MGI infrastructure: (i) nano structured polymeric materials and (ii) high temperature materials. This research thrust is in close collaboration with Professor Tresa Pollock and Professor Glenn Fredrickson.
Nanostructured Polymeric Materials
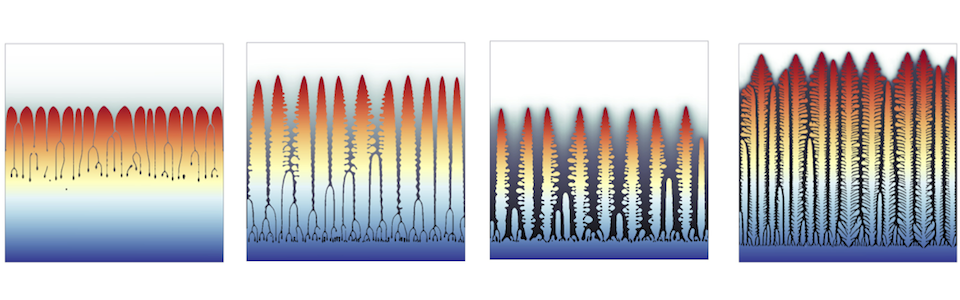
The past decade has been marked by dramatic advances in synthetic polymer chemistry, enabling unprecedented control over chain length, chain architecture, stereochemistry, and monomer sequence. These developments make it possible to construct block and graft copolymers with virtually any number of blocks or grafts in any archi- tecture and comprised from a broad pallet of commercially available monomers. Block and graft copolymers are capable of producing exquisite nanostructures by the phenomenon of microphase separation and have a myriad of applications in the energy, health and computer sectors. One of the challenges is to accurately describe thin structures along with large scale physics. Also, in the simplest AB class of block copolymers, with only two chemically distinct blocks, already five important nanostructures appear. Adding just one additional block type - the ABC family - introduces not only sequence complexity, but three types of binary interactions to manage and three independent block molecular weights. Associated with this enormous molecular design space are possibly hundreds or thousands of unique nanostructures, of which only about two dozen have been definitely identified. It is evident that accidental discovery of phases, or systematic brute-force searching through the enormous parameter spaces is not a viable path for materials by design. The following image depicts the results of a direct numerical computation of microphase separation (BCC, Cylindrical, Gyroid and Laminar):

High Temperature Multicomponent Alloys
Design advances in high temperature structural materials have been synonymous with advances in the performance and efficiency in power-generation turbines, aircraft, rocket engines, and nuclear power plants. The ability of these materials to withstand an increase in temperature by even a few degrees translates into a significant increase in energy efficiency. Further improvement in these systems are challenged by the fundamental barrier of the melting point of Ni-base alloys, which comprise a large fraction of all the critical high temperature components in these systems. While conducting Calphad-type assessments of the Co-Al-W system, Sato and co-workers discovered a stable ternary Co\(_{3}\)(Al,W) intermetallic compound with an ordered L1\(_{2}\) structure. This permits design of two phase microstructures that are morphologically identical to Ni-base superalloys and therefore likely to have exceptional high temperature properties. Pollock and co-workers, who conducted the early studies on processing and high temperature properties of these Co-base materials, have shown that they could deliver an increase in temperature capability greater than that achieved in Ni-base alloys over the past three generations combined. However, the large compositional space, ultimately likely to be comprised of combinations of 8 or more alloying elements, along with complex processing and performance constraints, make rapid development and deployment of this new class of materials a major challenge. The following image represents the map of the different growth regimes for a dilute Ni-Cu alloy, including growth regime transitions, obtained from our computations. This is the first time such a map is predicted numerically:
Computational Fluid Dynamics
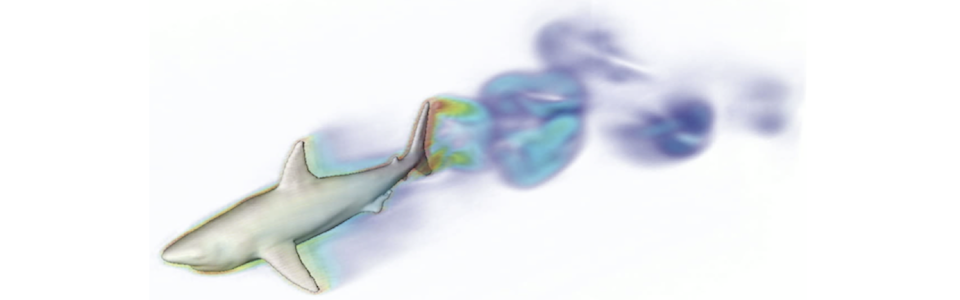
Computational Fluis Dynamics is concerned with the simulation and prediction of the motion of fluids, the forces generated and their coupling with other physical phenomena such as solidification, electrostatics, solid and elastic mechanics, etc. We are considering applications for both single and multiphase incompressible flows as well as compressible flows. One of the current thrust in our group is to understand the effects of fluid flows during solidification of multialloys and their potential impact on nucleation. Another thrust is to understand how the permeability is affected in the case of multiphase flows in porous media and the drag reduction on superhydrophobic surfaces. These research thrusts are in close collaboration with Professor Alban Sauret and Professor Paolo Luzzatto-Fegiz.
Flow Over Superhydrophobic Surfaces
Superhydrophobic Surfaces (SHS) have the potential to significantly reduce drag reduction. However, experimental work have shown disappointing results, underlying some gaps in the understanding of flows over SHS. With Professor Paolo Luzzatto-Fegiz and collaborators in France and the United Kigdom, we are engaged in a vigorous research program that focuses on understanding turbulent flows over SHS. In particular, simulations readily provide data that can be mined in order to derive models that capture the true momentum transfer from the outer flow to the solid ridges.
Flow in Reactive Porous Media
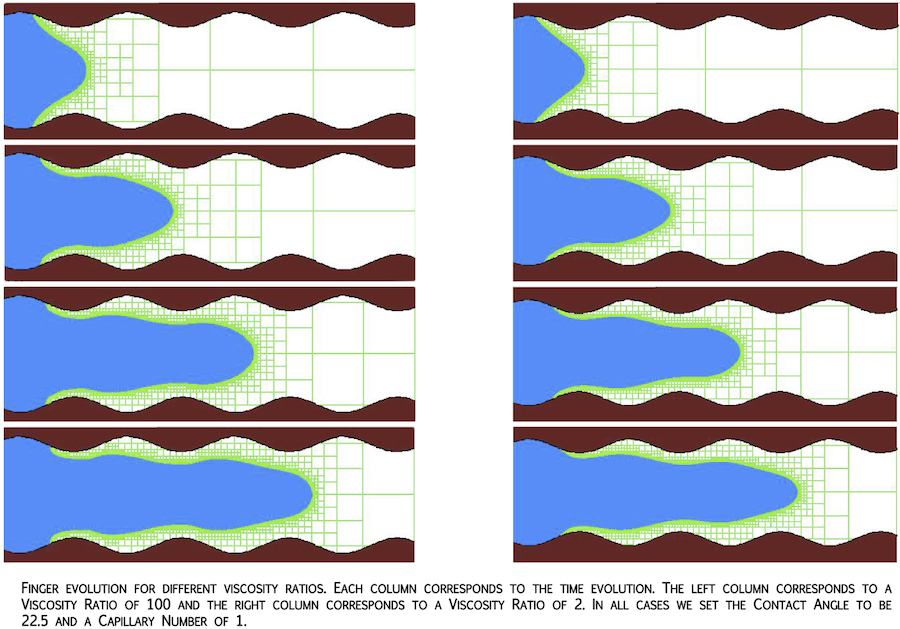
Flow in Reactive Porous Media where shrinkage and growth processes lead to a time and spatial evolution of the pores is of particular importance in many contexts ranging from oil recovery to CO2 sequestration. While flows in inert porous media have been thoroughly studied at the pore and macroscopic scales, the interplay between the evolution of the solid boundaries and the flow, and the multiscale nature in space and time of the phenomena, remains a significant challenge. We are studying this coupled situation with Professor Alban Sauret by designing and subsequently using Direct Numerical Simulations, and characterizing the time-evolution of the permeability, the possible clogging of pores, the flow rate, and the evolution of the particle spreading. This fundamental computational framework will enable us to perform a sequence of simulations, gradually increasing the complexity of the porous media from the scale of a single pore to porous media, and systematically characterizing the shrinkage and growth process as well as the flow-rate time evolution. The simulations seek to build a unique data set that will ultimately enable the discovery of new time-dependent permeability and tortuosity laws. The research is important because being able to couple the transport of a scalar quantity, such as the solute concentration, with moving boundaries remains challenging for classical numerical approaches. We are seeking to consider different reaction laws in pressure-driven and flow rate-driven flows and measure the local and average velocity field to build macroscopic quantities leading to an equivalent Darcy's law in evolving porous media.
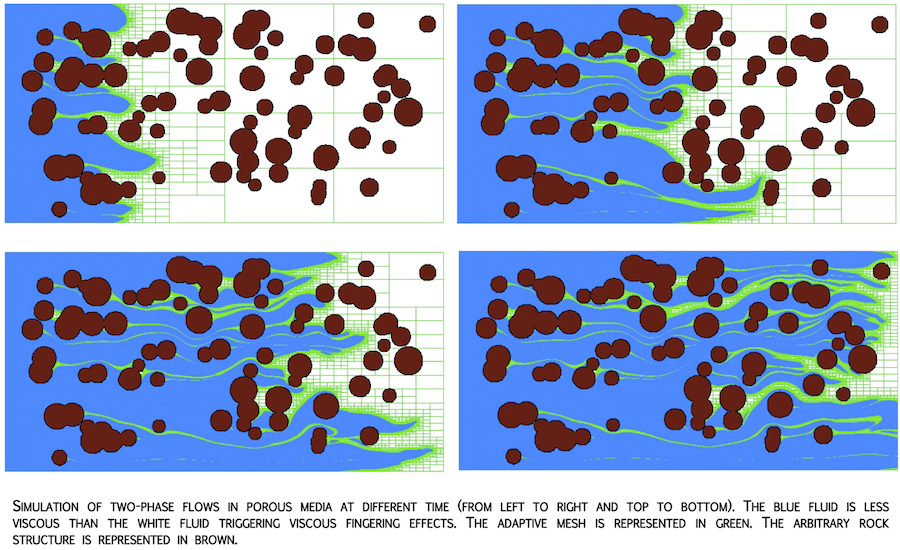
Multiphase Flows
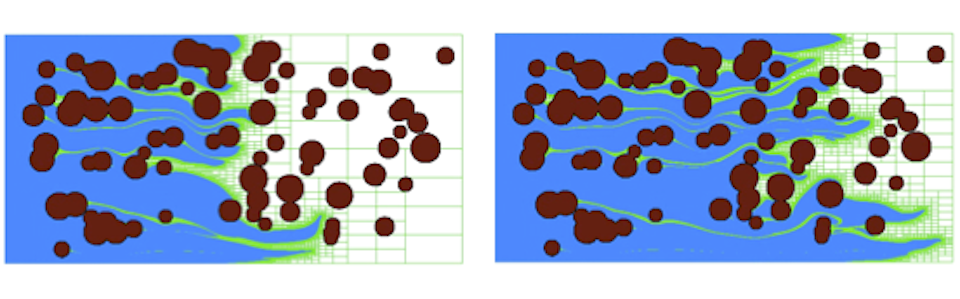
CO2 sequestration operations in deep subsurface geologic formations involve com- plex multiphase interactions that are not fully understood. This research project was aimed at developing such an understanding with focus on the detailed pore-scale physics and the development of a framework to translate the pore-scale physics to the Darcy and larger scales. To better understand the fluid-flow physics at the pore scale, we employed a level-set method that keeps track of the interface between the two immiscible fluids along with implicit representation of the pore-scale geometry. `Sharp' conditions at the contact-lines between fluids and at the solid boundaries were employed. The Octree adaptive mesh refinement framework was extended in order to solve this immiscible two-phase problem with reasonably good resolution. Computational results of the effects of capillary, viscous, and gravitational forces have been performed. Validation of our level-set approach for complex pore-scale rock geometries is ongoing.
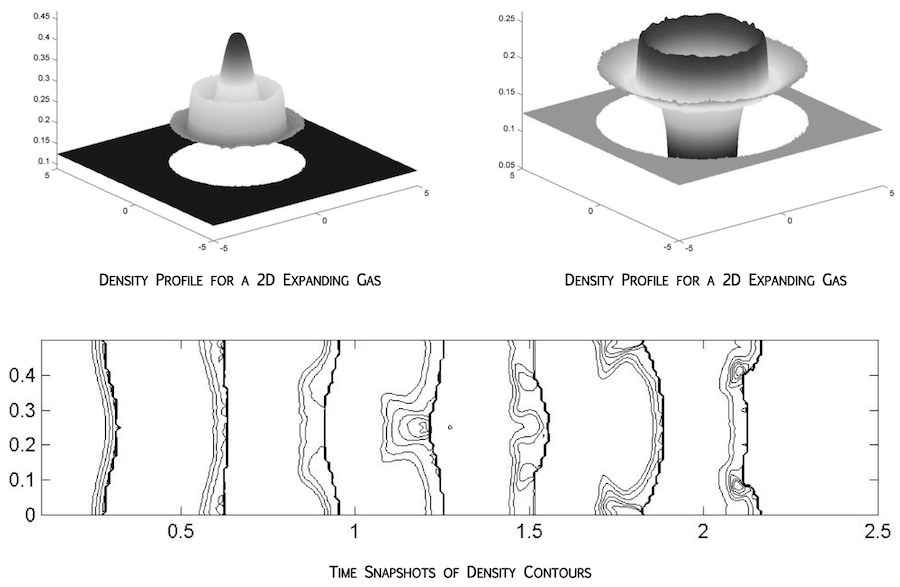
Compressible Reacting Flows
The main difficulties in the simulation of compressible reactive flows arise when the chemical reactions introduce time scales that are significantly shorter than the hydrodynamic time scales. Standard shock capturing algorithms smear out the front so that a few grid cells lie within the shock profile. The numerically smeared out temperature profile contains values that are artificially raised above the ignition temperature with the potential to trigger the chemical reaction too early. When the reaction is fast, the gas can be completely burnt in the next time step shifting the discontinuity to the adjacent cell boundary leading to a nonphysical one-grid-cell per time step spurious wave. We have designed a new, fully conservative version of the ghost fluid method applicable for tracking material interfaces, inert shocks, and both deflagration and detonation waves in as many as three spatial dimensions. The exact discrete conservation properties are most important when tracking inert shocks and detonation waves, so that is the focus of this paper. In particular, we address the inviscid reactive Euler equations in the context of stiff detonation waves on coarse grids. The main difficulty here arises when the time scales of the chemical reaction are significantly shorter than the time scales of the fluid dynamics leading to a stiff source term and nonphysical wave phenomena. We use the level set method to track the location of the detonation wave and the ghost fluid method to treat the discontinuous quantities across the inert shock portion of that wave. This leads to a sharp non-smeared shock profile alleviating the nonphysical wave phenomena.
Computational Image Analysis
Image Guided Surgery
Image guided surgery seeks to assist the surgeon in situation where the access to the organ to be operated on is limited. An example is the surgery in the lungs where instruments are inserted in the bronchi and imaging is performed to help locate the desired point of operation. The strategy is perform a detailed 3D CT-scan prior to the surgery and then use less toxic imaging techniques (such as fluoroscopy) during the surgery. The 3D to 2D registration algorithm to recover the Pose (position and orientation) and the tracking algorithms to follow instruments during surgery is one of the main challenges. Fast algorithms need to be design since real-time procedures are sought. We have used our computational framework on Octrees to construct a Digitally Reconstructed Radiography (DRR) from the 3D CT-scan that can then be registered to the 2D x-ray fluoroscopy
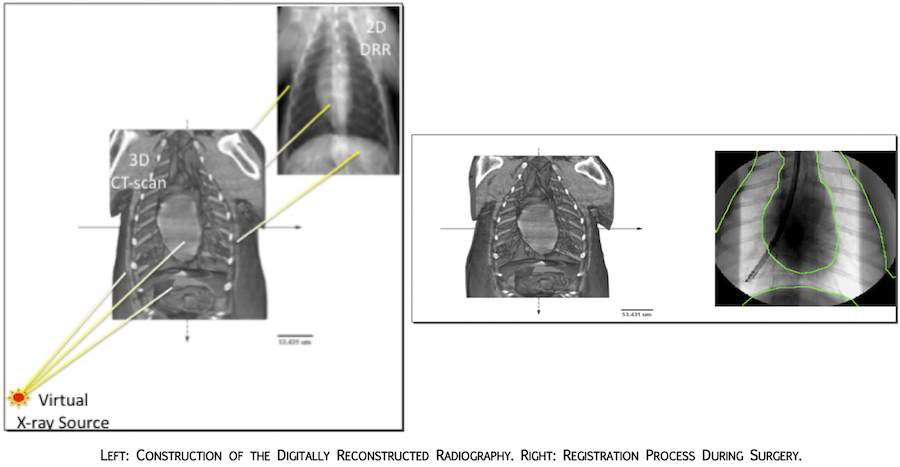
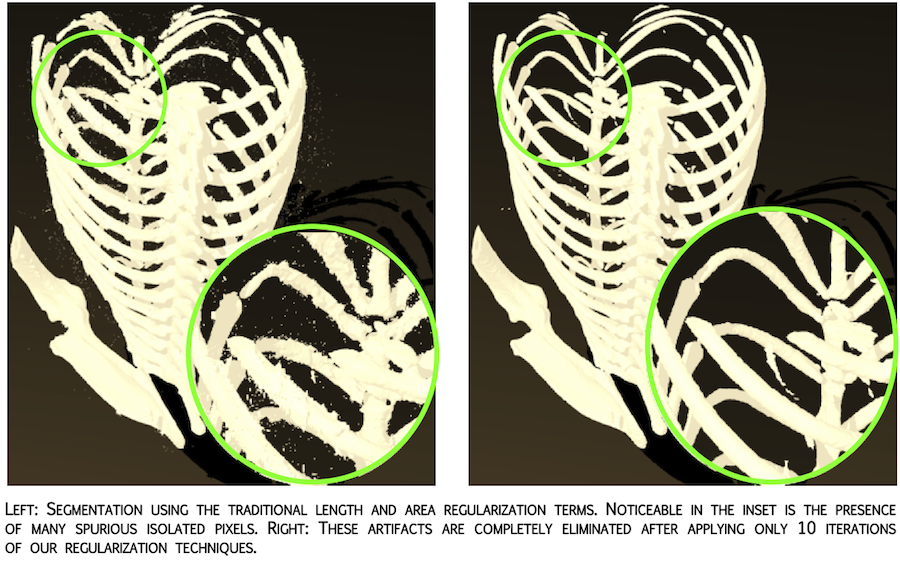
Image Segmentation
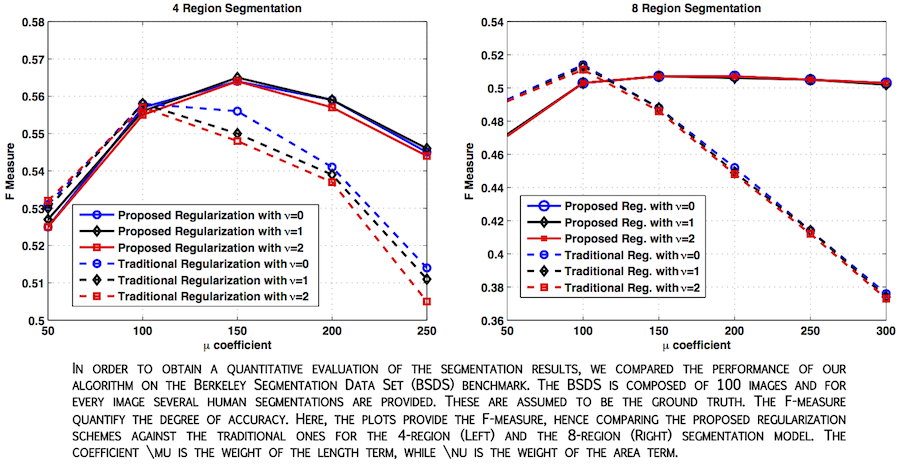
Image segmentation is part of any image processing analysis. The level-set has been a very successful tool in that subject. In the case where several distinct regions need to be segmented, regularization must be introduced in a different way as in the two regions. We have introduced novel regularization techniques for level-set segmentation that target specifically the problem of multiphase segmentation. When the multiphase model is used to obtain a partitioning of the image in more than two regions, a new set of issues arise with respect to the single phase case in terms of regularization strategies. For example, if smoothing or shrinking each contour individually 0 could be a good model in the single phase case, this does not necessarily holds true in the multiphase scenario. We have addressed these issues designing novel length and area regularization terms, whose minimization yields evolution equations in which each level-set function involved in the multiphase segmentation can "sense" the presence of the other level-set functions and evolve accordingly. The coupling of the level set function, which before was limited to the data term (i.e. the proper segmentation driving force), is extended in a mathematically principled way to the regularization terms as well. The resulting regularization technique is more suitable to eliminate spurious regions and other kind of artifacts. An extensive experimental evaluation supports our model, showing improved segmentation performance with respect to traditional regularization techniques.