


Next: An SIS model with
Up: APC/EEB/MOL 514 Tutorial 4:
Previous: Introduction
Let 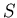 be the number of susceptible individuals, and let
be the number of susceptible individuals, and let 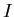 be the
number of infected individuals. For an SIS model, infected individuals
return to the susceptible class on recovery because the disease confers
no immunity against reinfection. (For the SIR model covered in lecture,
recovered individuals instead pass to the class R upon
recovery.) The simplest SIS model is given by
be the
number of infected individuals. For an SIS model, infected individuals
return to the susceptible class on recovery because the disease confers
no immunity against reinfection. (For the SIR model covered in lecture,
recovered individuals instead pass to the class R upon
recovery.) The simplest SIS model is given by
Let's briefly explore the meaning of these terms.
- The
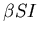 term is understood as follows:
An average infected individual makes contact sufficient to infect
term is understood as follows:
An average infected individual makes contact sufficient to infect 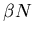 others per unit time. Also, the probability that a given individual that
each infected individual comes in contact with is susceptible is
others per unit time. Also, the probability that a given individual that
each infected individual comes in contact with is susceptible is 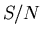 .
Thus, each infected individual causes
.
Thus, each infected individual causes
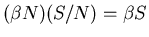 infections
per unit time. Therefore,
infections
per unit time. Therefore, 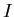 infected individuals cause a total
number of infections per unit time of
infected individuals cause a total
number of infections per unit time of 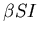 .
.
- The
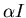 term is even simpler to understand:
term is even simpler to understand: 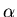 is the fraction
of infected individuals who recover (and re-enter the susceptible class)
per unit time.
is the fraction
of infected individuals who recover (and re-enter the susceptible class)
per unit time.
We see that
so
Here 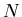 is the total population. Substituting
is the total population. Substituting 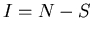 into (2),
we obtain
into (2),
we obtain
Solving 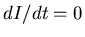 , we see that there are two possible equilibria for this
SIS model, one with
, we see that there are two possible equilibria for this
SIS model, one with 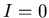 and the other with
and the other with
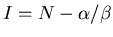 .
Defining the basic reproductive number as
.
Defining the basic reproductive number as
it can be shown that
-
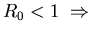 the equilibrium with
the equilibrium with 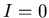 is stable,
is stable,
-
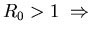 the equilibrium with
the equilibrium with
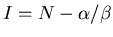 is stable.
is stable.



Next: An SIS model with
Up: APC/EEB/MOL 514 Tutorial 4:
Previous: Introduction
Jeffrey M. Moehlis
2002-10-14
![]() be the number of susceptible individuals, and let
be the number of susceptible individuals, and let ![]() be the
number of infected individuals. For an SIS model, infected individuals
return to the susceptible class on recovery because the disease confers
no immunity against reinfection. (For the SIR model covered in lecture,
recovered individuals instead pass to the class R upon
recovery.) The simplest SIS model is given by
be the
number of infected individuals. For an SIS model, infected individuals
return to the susceptible class on recovery because the disease confers
no immunity against reinfection. (For the SIR model covered in lecture,
recovered individuals instead pass to the class R upon
recovery.) The simplest SIS model is given by