Architecture of Distributed Control Design

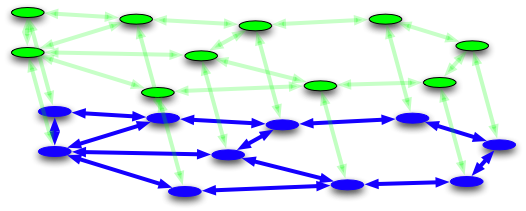Control design with pre-specified information passing structure

The blue layer represents a distributed dynamical system and its interaction links, while the green nodes and arrows represent a distributed controller with pre-constrained information passing links (between controller sites) and sensing/actuation links. For many reasons, it is desirable to design optimal spatially distributed controllers with such pre-sepcified constraints on their communication requirements. The exact problem is non-convex in general, but there are certain important cases that correspond to convex problem (see below). Interestingly, in some cases the optimal controller inherits the plant's constraint structure for free (even when not explicitly imposed in the optimization problem).

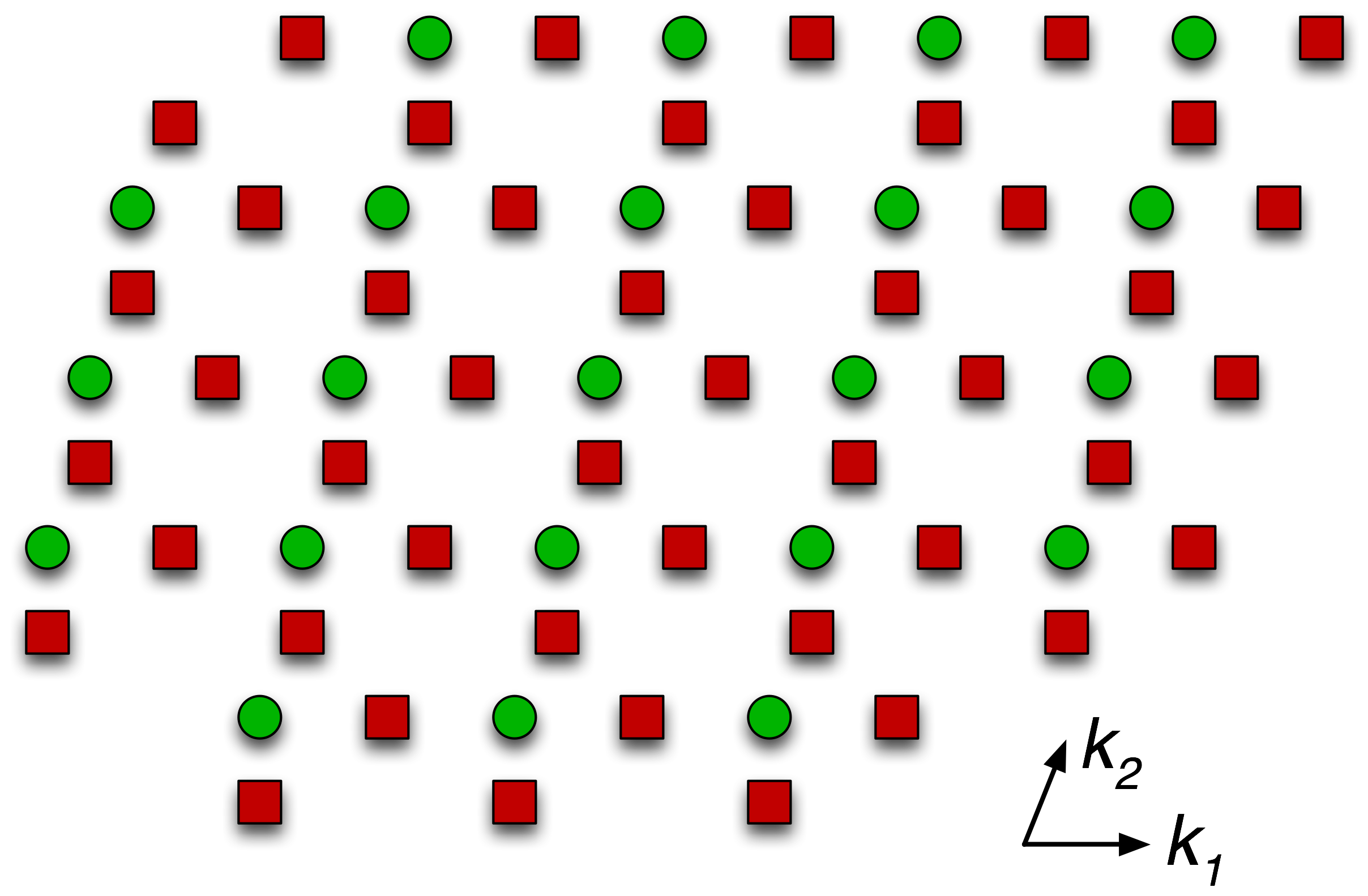Optimal controllers inherit plant's symmetries

When the plant has certain symmetries, i.e. its dynamics are invariant under the action of some symmetry group, controllers inhert some of that symmetry automatically. It can be shown that an optimal controller with the same symmetries of the plant can be designed when the performance index is any closed loop norm that is also symmetric (see the paper). The basic argument is a generalization to the spatial case of an averaging argument used to investigate time varying versus time invariant controllers in the paper by Shamma & Dahleh. This in turn is based on the averaging arguments used to construct the invariant Haar measure on groups.

Incidentally, it appears that this principle is violated when one considers non-norm performance measures, or when a-priori structural constraints are placed on the controller. For an example of this, see the “symmetry breaking” or “Mistuning” control design for platoons.

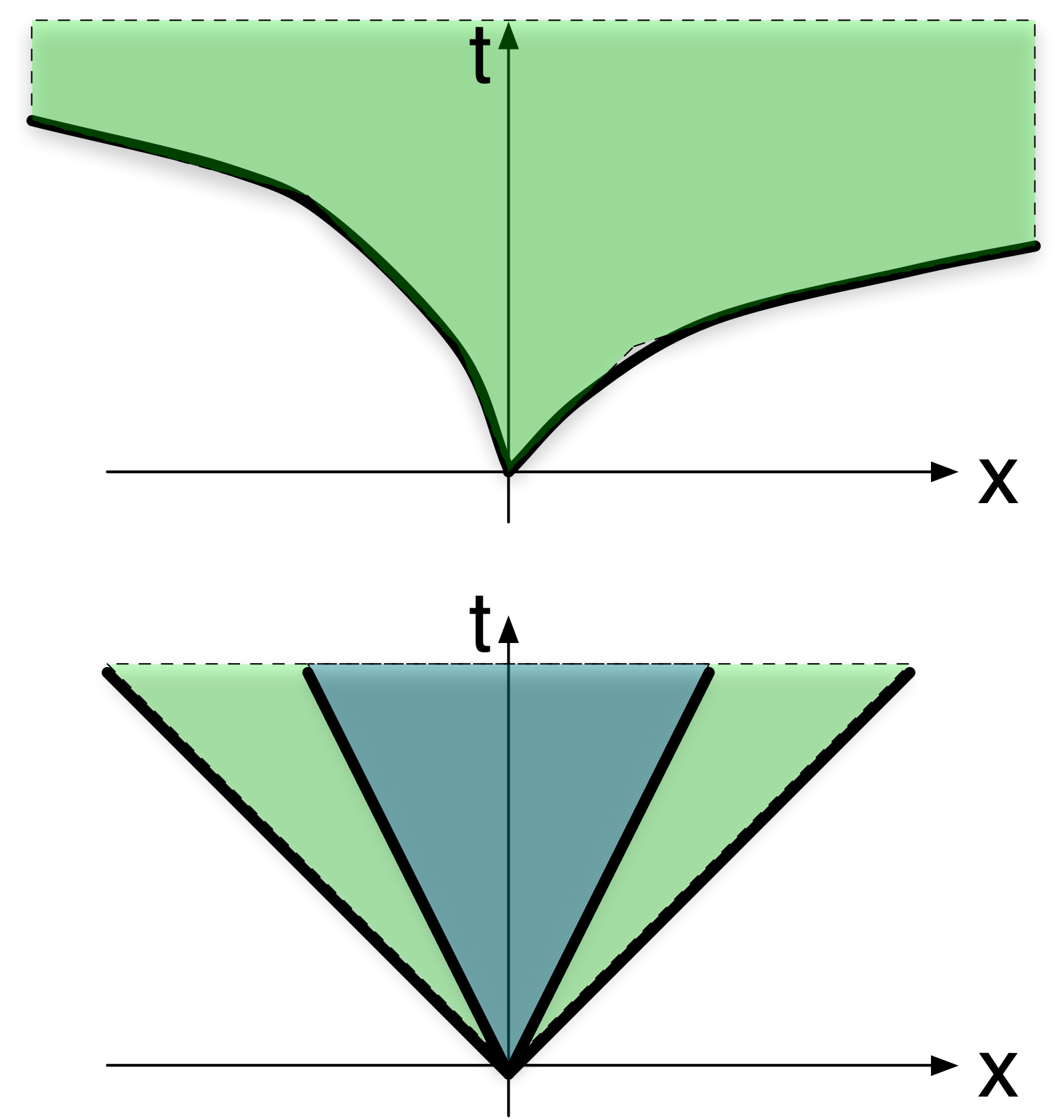Controller information propagating faster than plant dynamics

The “speed” at which information/effects travel in a spatio-temporal system can be visualized using their spatio-temporal impulse response. The diagram on the left gives an example of a support set for a spatio-temporal impulse response. We call this “funnel causality”. The (t,x) funnel illustrates the first time t at which dynamical effects arrive at a site a distance x away in a spatially invariant system. The diagram on the right illustrates an optimal control design problem with apriori spatio-temporal causality restrictions. The blue funnel represents the plant, and the green funnel represents the class of controllers. When information passing in the controller is at least as fast as that in the plant (i.e. the controller's funnel includes the plant's funnel), the constrained optimal controller design problem is convex!

This fact was first observed for spatially invariant systems with distributed delayed measurements, and is actually based on the earlier work of Voulgaris. The notion of Quadratic Invariance is a generalization to a larger class of problems. The above interpretation in terms of speed of information travel in controller versus that in the plant was first given for the special class of spatially invariant systems. Rotkowitz, Cogill & Lall obtained a similar statement for a more general class of networks in which a natural notion of distance can be formulated.

Quadratically optimal controllers are inherently localized!

For spatially distributed control design, a central question is the nature of the spatial interconnectedness of optimal controllers. It is perhaps a surprise that quadratically optimal controllers designed with no a-priori constraints (i.e. the centralized controller), turn out to have some inherent localization properties. It can be shown that for most spatially invariant plants, quadratically optimal controllers have state feedback and observer gains that decay exponentially with distance, making them effectively localized. The example on the left is the centralized LQR state-feedback gain for a string network of size 50.

See the paper for the spatially invariant case, and the recent work by Motee & Jadbabaie for a far-reaching generalization of this concept.