Figures from
Model Predictive Control: Theory, Computation, and Design

2nd Edition

James B. Rawlings	David Q. Mayne	Moritz M. Diehl
Department of Chemical Engineering	Department of Electrical and Electronic Engineering	Department of Microsystems Engineering
University of California	Imperial College London	University of Freiburg
Santa Barbara, California, USA	London, England	Freiburg, Germany

Click on thumbnails to enlarge figures and display Octave/Matlab code and data. You will also need a few files (mostly for plotting) that are only included in the tar.gz or zip files linked below, so if you want to run them, the best thing to do is download the complete collection of M-files! Having the code linked here is still useful if you want to take a quick look at how something is done.

Running the example files requires Octave (version 4.0 or later) or Matlab (R2015a or later), as well as CasADi (version 3.0 or later; download here) and MPCTools (download here). Installation instructions can be found on the respective websites.

Complete collections of the M-files for both Octave and Matlab in zip file formats are available for download from the following links:

Octave (v2.3)

Matlab (v2.3)

Chapter 1: Getting Started with Model Predictive Control

	Figure 1.3 (page 10): Output of a stochastic system versus time.				Figure 1.4 (page 15): Two quadratic functions and their sum.
	Figure 1.8 (page 57): Three measured outputs versus time after a step change in inlet flowrate at 10 minutes; n_d=2.				Figure 1.9 (page 57): Two manipulated inputs versus time after a step change in inlet flowrate at 10 minutes; n_d=2.
	Figure 1.10 (page 58): Three measured outputs versus time after a step change in inlet flowrate at 10 minutes; n_d=3.				Figure 1.11 (page 59): Two manipulated inputs versus time after a step change in inlet flowrate at 10 minutes; n_d=3.

Chapter 2: Model Predictive Control---Regulation

	Figure 2.1 (page 101): Example of MPC.				Figure 2.2 (page 102): Feasible region \mathcal {U}_2, elliptical cost contours and ellipse center a(x), and constrained minimizers for different values of x.
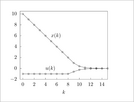
	Figure 2.3 (page 106): First element of control constraint set \mathcal {U}_3(x) (shaded) and control law \kappa _3(x) (line) versus x=(\cos (\theta ),\sin (\theta )), \theta \in [-\pi ,\pi ] on the unit circle for a nonlinear system with terminal constraint.				Figure 2.4 (page 107): Optimal cost V_3^0(x) versus x on the unit circle.
	Figure 2.5 (page 159): Closed-loop economic MPC versus tracking MPC starting at x=(-8,8) with optimal steady state (8,4). Both controllers asymptotically stabilize the steady state. Dashed contours show cost functions for each controller.				Figure 2.6 (page 160): Closed-loop evolution under economic MPC. The rotated cost function \tilde {V}^0 is a Lyapunov function for the system.
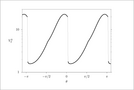
	Figure 2.8 (page 164): Feasible sets \mathcal {X}_N for two values of \dot {Q}_min. Note that for \dot {Q}_min=9 (right-hand side), \mathcal {X}_N for N \leq 4 are disconnected sets.				Figure 2.9 (page 165): Phase portrait for closed-loop evolution of cooler system with \dot {Q}_min=9. Line colors show value of discrete actuator u_2.
	Figure 2.10 (page 174): Region of attraction (shaded region) for constrained MPC controller of Exercise \ref {exer:Xnterminal}.				Figure 2.11 (page 175): The region \mathbb {X}_f, in which the unconstrained LQR control law is feasible for Exercise \ref {exer:Xinf}.
	Figure 2.12 (page 177): The region of attraction for terminal constraint x(N) \in \mathbb {X}_f and terminal penalty V_f(x)=(1/2)x' \Pi x and the estimate of \bar {\mathcal {X}}_N for Exercise \ref {exer:NoTerminal}.				Figure 2.15 (page 185): Rotated cost-function contour \tilde {\ell }(x,u)=0 (circles) for \lambda = 0, -8, -12. Shaded region shows feasible region where \tilde {\ell }(x,u)<0.

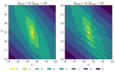
Chapter 3: Robust Model Predictive Control

	Figure 3.4 (page 232): Minimum feasible \alpha for varying N. Note that we require \alpha \in [0, 1).				Figure 3.5 (page 233): Bounds on tightened constraint set \bar {\mathbb {Z}} for varying N. Bounds are \left \| x_1 \right \| \le \chi _1, \left \| x_2 \right \| \le \chi _2, and \left \| u \right \| \le \mu .
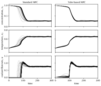
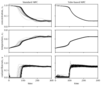
	Figure 3.6 (page 244): Comparison of 100 realizations of standard and tube-based MPC for the chemical reactor example.				Figure 3.7 (page 245): Comparison of standard and tube-based MPC with an aggressive model predictive controller.
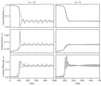
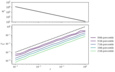
	Figure 3.8 (page 246): Concentration versus time for the ancillary model predictive controller with sample time \Delta =12 (left) and \Delta =8 (right).				Figure 3.9 (page 255): Observed probability \varepsilon _test of constraint violation for i=10. Distribution is based on 500 trials for each value of \varepsilon . Dashed line shows the outcome predicted by formula \eqref {eq:tempoformula}, i.e., \varepsilon _test = \varepsilon .
	Figure 3.10 (page 263): Closed-loop robust MPC state evolution with uniformly distributed \left \| w \right \| \leq 0.1 from four different x_0.

Chapter 4: State Estimation

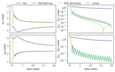
	Figure 4.2 (page 300): Comparison of filtering and smoothing updates for the batch reactor system. Second column shows absolute estimate error.				Figure 4.3 (page 308): Evolution of the state (solid line) and EKF state estimate (dashed line).
	Figure 4.4 (page 309): Evolution of the state (solid line) and UKF state estimate (dashed line).				Figure 4.5 (page 310): Evolution of the state (solid line) and MHE state estimate (dashed line).
	Figure 4.7 (page 317): Closed-loop performance of combined nonlinear MHE/MPC with no disturbances. First column shows system states, and second column shows estimation error. Dashed line shows concentration setpoint. Vertical lines indicate times of setpoint changes.				Figure 4.8 (page 318): Closed-loop performance of combined nonlinear MHE/MPC for varying disturbance size. The system is controlled between two steady states.

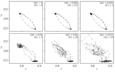
Chapter 6: Distributed Model Predictive Control

	Figure 6.2 (page 397): Ten iterations of noncooperative steady-state calculation.				Figure 6.3 (page 397): Ten iterations of cooperative steady-state calculation.
	Figure 6.4 (page 398): Ten iterations of noncooperative steady-state calculation; reversed pairing.				Figure 6.5 (page 398): Ten iterations of cooperative steady-state calculation; reversed pairing.
	Figure 6.7 (page 416): Cost contours for a two-player, nonconvex game.				Figure 6.8 (page 419): Nonconvex function optimized with the distributed gradient algorithm.
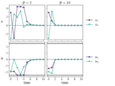
	Figure 6.9 (page 424): Closed-loop state and control evolution with (x_1(0),x_2(0)) = (3,-3).				Figure 6.10 (page 425): Contours of V(x(0),\mathbf {u}_1,\mathbf {u}_2) for N=1.

Chapter 7: Explicit Control Laws for Constrained Linear Systems

Figure 7.6 (page 462):
Regions R_x,\ x \in X for a second-order example.

Figure 7.8 (page 480):
Solution times for explicit and implicit MPC for N = 20.

Chapter 8: Numerical Optimal Control

	Figure 8.1 (page 490): Feasible set and reduced objective \psi (u(0)) of the nonlinear MPC Example~\ref {ex:nc-nl-mpc}.				Figure 8.2(a) (page 499): Performance of different integration methods. Accuracy vs. function evaluations.
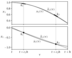
	Figure 8.2(b) (page 499): Performance of different integration methods. Simulation results for M=32.				Figure 8.3 (page 504): Polynomial approximation \tilde {x}_1(t) and true trajectory x_1(t) of the first state and its derivative.
	Figure 8.4(a) (page 506): Performance of implicit integration methods on a stiff ODE. Accuracy vs. collocation points.				Figure 8.4(b) (page 506): Performance of implicit integration methods on a stiff ODE. Simulation result for M=10 points.
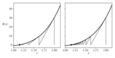
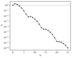
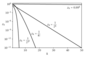
	Figure 8.5 (page 510): Newton-type iterations for solution of R(z)=0 from Example~\ref {ex:num-newton-fifth-root}. Left: exact Newton method. Right: constant Jacobian approximation.				Figure 8.6 (page 512): Convergence of different sequences as a function of k.
	Figure 8.7 (page 578): Relaxed and binary feasible solution for Example~\ref {ex:nc-binary}.				Figure 8.8 (page 585): A hanging chain at rest. See Exercise~\ref {ex:hanging_chain}\ref {sub:hc}.
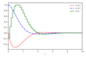
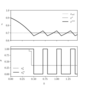
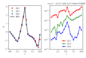
	Figure 8.9 (page 587): Direct single shooting solution for \eqref {eq:vdp} without path constraints.				Figure 8.10 (page 590): Open-loop simulation for \eqref {eq:vdp} using collocation.
	Figure 8.11 (page 592): Gauss-Newton iterations for the direct multiple-shooting method

Figures from Model Predictive Control: Theory, Computation, and Design