Figures from
Modeling and Analysis Principles for Chemical and Biological Engineers

2nd Edition

Michael D. Graham		James B. Rawlings
Department of Chemical and Biological Engineering		Department of Chemical Engineering
University of Wisconsin		University of California, Santa Barbara
Madison, Wisconsin		Santa Barbara, California

Copyright (C) 2026 Nob Hill Publishing, LLC

Click on thumbnails to enlarge figures and display Python code and data. You will also need a few files (mostly for plotting) that are included only in the zip files linked below, so if you want to run them, the best thing to do is download the complete collection of .py-files! Having the code linked here is still useful if you want to take a quick look at how something is done.

A complete collection of the .py-files for Python in zip file formats is available for download from the following link:

Python (v1.0)

Octave/Matlab Legacy Code.

Complete collections of the .m-files for both Octave and Matlab in zip file formats are available for download from the following links. Note: these .m-files were current as of 10/2024. They are no longer maintained.

Octave (v1.5)

Matlab (v1.5)

Chapter 1: Linear Algebra

	Figure 1.3 (page 32): An iteration of the Newton-Raphson method for solving f(x)=0 in the scalar case.				Figure 1.6 (page 61): Contours of constant f(x)=x^TAx.
	Figure 1.8 (page 75): Experimental measurements of variable y versus x.				Figure 1.9 (page 77): Measured rate constant at several temperatures.
	Figure 1.10 (page 85): Plot of Ax as x moves around a unit circle.

Chapter 2: Ordinary Differential Equations

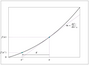
	Figure 2.1 (page 106): Dynamical regimes for the planar system dx/dt = Ax, A \in \mathbb {R}^{2 x2}.				Figure 2.2 (page 107): Dynamical behavior on the region boundaries for the planar system dx/dt = Ax, A \in \mathbb {R}^{2 x2}.
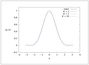
	Figure 2.4 (page 127): Function f(x)=\exp \big (-8\big (\frac {x}{\pi }\big )^{2}\big ) and truncated trigonometric Fourier series approximations with K=2,5,10. The approximations with K=5 and K=10 are visually indistinguishable from the exact function.				Figure 2.5 (page 128): Truncated trigonometric Fourier series approximation to f(x)=x, using K=5,10, 50. The wiggles get finer as K increases.
	Figure 2.6 (page 130): Function f(x)=\exp \big (-8x^{2}\big ) and truncated Legendre-Fourier series approximations with n=2,5,10.				Figure 2.7 (page 131): Function f(x)=H(x) and truncated Legendre-Fourier series approximations with n=10,50,100.
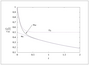
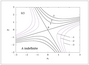
	Figure 2.12 (page 176): Leading-order inner U_0, outer u_0, and composite solutions u_{0c}, for Example \ref {ex:rxequil} with \epsilon =0.2, K=1, and k_{2}=1.				Figure 2.15 (page 187): Contours of an energy function V(x_{1},x_{2}) or H(x_{1},x_{2}).
	Figure 2.16 (page 191): Energy landscape for a pendulum; H = \frac {1}{2} p^2 -\kappa \cos q; \kappa =2.				Figure 2.17 (page 192): Landscape for H=\frac {1}{2}p^{2}+\frac {1}{4}q^{4}-\frac {1}{2}q^{2}.
	Figure 2.18 (page 194): A limit cycle (thick dashed curve) and a trajectory (thin solid curve) approaching it.				Figure 2.19 (page 196): Periodic (left) and quasiperiodic (right) orbits on the surface of a torus. The orbit on the right eventually passes through every point in the domain.
	Figure 2.20 (page 197): A limit cycle for the R\"ossler system, a=b=0.2, c=1.				Figure 2.21 (page 197): A strange attractor for the R\"ossler system, a=b=0.2, c=5.7.
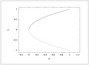
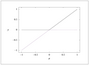
	Figure 2.22 (page 199): Bifurcation diagram for the saddle-node bifurcation.				Figure 2.23 (page 201): Bifurcation diagram for the transcritical bifurcation.
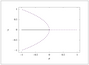
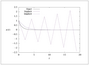
	Figure 2.24 (page 202): Bifurcation diagrams for the pitchfork bifurcation.				Figure 2.25 (page 207): Approximate solutions to \dot {x}=-x using explicit and implicit Euler methods with \Delta t=2.1, along with the exact solution x(t)=e^{-t}.
	Figure 2.26 (page 210): Stability regions for Adams-Bashforth methods; \dot {x}=\lambda x.				Figure 2.27 (page 211): Stability regions for Adams predictor-corrector methods; \dot {x}=\lambda x.
	Figure 2.28 (page 212): Stability regions for Runge-Kutta methods; \dot {x}=\lambda x.				Figure 2.29 (page 215): Hat functions for N=2.
	Figure 2.30 (page 216): Approximate solutions to \eqref {eq:MWRexample} using the finite element method with hat functions for N=6 and N=12. The exact solution also is shown.				Figure 2.31 (page 220): Dependence of \left | c(j) \right | on j for the Legendre-Galerkin approximation of \eqref {eq:MWRexample} with n=10.
	Figure 2.34 (page 242): Stability regions for Adams predictor-corrector methods; \dot {x}= \lambda x; APCn' uses nth-order predictor and nth-order corrector.

Chapter 3: Vector Calculus and Partial Differential Equations

Figure 3.12 (page 320): Concentration versus membrane penetration distance for different reaction rate constants.

Figure 3.13 (page 341): Transient heating of slab, cylinder, and sphere.

Chapter 4: Probability, Random Variables, and Estimation

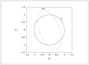
	Figure 4.1 (page 365): Normal distribution, with probability density p_\xi (x) = (1/\sqrt {2\pi \sigma ^2}) \exp (-(1/2) (x-m)^2/\sigma ^2).				Figure 4.2 (page 370): Multivariate normal for n=2. The contour lines show ellipses containing 95, 75, and 50 percent probability.
	Figure 4.5 (page 383): A joint density function for the two uncorrelated random variables in Example~\ref {ex:jointunc}.				Figure 4.6 (page 387): A nearly singular normal density in two dimensions.
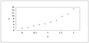
	Figure 4.8 (page 394): Histogram of 10,000 samples of uniformly distributed x.				Figure 4.9 (page 394): Histogram of 10,000 samples of \displaystyle y=\DOTSB \sum@ \slimits@ _{i=1}^{10} x_i .
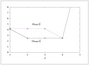
	Figure 4.10 (page 409): The multivariate normal, marginals, marginal box, and bounding box.				Figure 4.11 (page 433): The sum of squares fitting error (top) and validation error (bottom) for PCR versus the number of principal components \ell ; cross validation indicates that four principal components are best.
	Figure 4.12 (page 434): The sum of squares validation error for PCR and PLSR versus the number of principal components/latent variables \ell ; note that only two latent variables are required versus four principal components.				Figure 4.13 (page 435): Predicted versus measured outputs for the validation dataset. Top: PCR using \textit {four} principal components. Bottom: PLSR using \textit {two} latent variables. Left: first output. Right: second output.
	Figure 4.14 (page 436): Effect of undermodeling. Top: PCR using \textit {three} principal components. Bottom: PLSR using \textit {one} latent variable.				Figure 4.15 (page 439): The indicator (step) function f_1(w;x) and its smooth approximation, f(w;x).
	Figure 4.16 (page 455): Typical strain versus time data from a molecular dynamics simulation. The data are available on the website \jbrawweb .				Figure 4.17 (page 456): Plot of y versus x available on the website \jbrawweb .
	Figure 4.18 (page 462): Smooth approximation to a unit step function, H(z-1).

Chapter 5: Stochastic Models and Processes

	Figure 5.2 (page 474): Sampling faster on the last plot in Figure \ref {fig:wiener}; the sample time is decreased to \Delta t = 10^{-9} and the roughness is restored on this time scale.				Figure 5.3 (page 481): A representative trajectory of the discretely sampled Brownian motion; D=2, V=0, n=500.
	Figure 5.4 (page 481): The mean square displacement versus time; D=2, V=0, n=500.				Figure 5.5 (page 489): Two first-order reactions in series in a batch reactor, c_{A0}=1, c_{B0}=c_{C0}=0, k_1=2, k_2=1.
	Figure 5.6 (page 491): A sample path of the unit Poisson process.				Figure 5.7 (page 491): A unit Poisson process with more events; sample path (top) and frequency distribution of event times \tau .
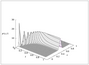
	Figure 5.9 (page 498): Stochastic simulation of first-order series reaction A-> B-> C starting with 100 A molecules.				Figure 5.11 (page 502): Solution to master equation for A + B <-> C starting with 20 A molecules, 100 B molecules and 0 C molecules, k_1=1/20, k_{-1}=3.
	Figure 5.12 (page 503): Solution to master equation for A + B <-> C starting with 200 A molecules, 1000 B molecules and 0 C molecules, k_1=1/200, k_{-1}=3.				Figure 5.13 (page 505): The equilibrium reaction extent's probability density for Reactions \ref {rxn:rxn2} at system volume \Omega =20 (top) and \Omega = 200 (bottom). Notice the decrease in variance in the reaction extent as system volume increases.
	Figure 5.14 (page 509): Simulation of 2 A \mathrel {\mkern 4mu}\mathrel {\smash {\mathchar "392D}}\mathrel {\mkern -2.5mu}-> B for n_0=500, \Omega =500. Top: discrete simulation; bottom: SDE simulation.				Figure 5.15 (page 510): Cumulative distribution for 2 A \mathrel {\mkern 4mu}\mathrel {\smash {\mathchar "392D}}\mathrel {\mkern -2.5mu}-> B at t=1 with n_0=500, \Omega =500. Discrete master equation (steps) versus omega expansion (smooth).
	Figure 5.16 (page 524): The change in 95% confidence intervals for \hat {x}(k\vert k) versus time for a stable, optimal estimator. We start at k=0 with a large initial variance P(0), which gives a large confidence interval.				Figure 5.17 (page 534): Deterministic simulation of reaction A + B <-> C compared to stochastic simulation.